Refine listing
Actions for selected content:
1959 results in 20xxx
COMPLETELY REGULAR MONOIDS WITH TWO GENERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 271-287
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Groups with few conjugacy classes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 31 March 2011, pp. 423-430
-
- Article
-
- You have access
- Export citation
On conditional permutability and saturated formations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 309-319
-
- Article
-
- You have access
- Export citation
PROPERTY (FA) OF THE GAUSS–PICARD MODULAR GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 225-228
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
TETRAVALENT ARC-TRANSITIVE GRAPHS WITH UNBOUNDED VERTEX-STABILIZERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 79-89
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Primitivity testing of finite nilpotent linear groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 March 2011, pp. 87-98
-
- Article
-
- You have access
- Export citation
Is the function field of a reductive Lie algebra purely transcendental over the field of invariants for the adjoint action?
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 01 February 2011, pp. 428-466
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Growth in Baumslag–Solitar groups I: subgroups and rationality
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 February 2011, pp. 34-71
-
- Article
-
- You have access
- Export citation
Dehn surgeries on some classical links
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 33-45
-
- Article
-
- You have access
- Export citation
Surface groups within Baumslag doubles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 91-97
-
- Article
-
- You have access
- Export citation
Cubic graphs admitting transitive non-abelian characteristically simple groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 113-123
-
- Article
-
- You have access
- Export citation
Fixed-point free action of an abelian group of odd non-squarefree exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 77-89
-
- Article
-
- You have access
- Export citation
THE IDEAL STRUCTURE OF SEMIGROUPS OF TRANSFORMATIONS WITH RESTRICTED RANGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 09 December 2010, pp. 289-300
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
ON THE PARTITION MONOID AND SOME RELATED SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 273-288
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
POSITIVE LAWS ON LARGE SETS OF GENERATORS: COUNTEREXAMPLES FOR INFINITELY GENERATED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 01 April 2011, pp. 289-296
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON COMMON DIVISORS OF MULTINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 13 October 2010, pp. 138-157
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
LIFTS OF PARTIAL CHARACTERS WITH CYCLIC DEFECT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 November 2010, pp. 145-163
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ON RESIDUALLY FINITE VARIETIES OF INVOLUTION SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 December 2010, pp. 181-198
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
A CONDITION IN FINITE SOLVABLE GROUPS RELATED TO CYCLIC SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 267-272
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Topological complexity of collision-free motion planning on surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 649-660
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
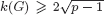 with equality if and only if if
with equality if and only if if 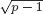 is an integer,
is an integer, 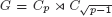 and
and 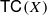 is a numerical homotopy invariant of a topological space
is a numerical homotopy invariant of a topological space 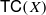 measures the complexity of motion planning algorithms which can be designed for the system. In this paper, we compute the topological complexity of the configuration space of
measures the complexity of motion planning algorithms which can be designed for the system. In this paper, we compute the topological complexity of the configuration space of 