Let G be a finite group and let H≤G. We refer to |H||CG(H)| as the Chermak–Delgado measure ofH with respect to G. Originally described by Chermak and Delgado, the collection of all subgroups of G with maximal Chermak–Delgado measure, denoted 𝒞𝒟(G), is a sublattice of the lattice of all subgroups of G. In this paper we note that if H∈𝒞𝒟(G)then H is subnormal in G and prove that if K is a second finite group then 𝒞𝒟(G×K)=𝒞𝒟(G)×𝒞𝒟(K) . We additionally describe the 𝒞𝒟(G≀Cp)where G has a nontrivial centre and p is an odd prime and determine conditions for a wreath product to be a member of its own Chermak–Delgado lattice. We also examine the behaviour of centrally large subgroups, a subset of the Chermak–Delgado lattice.

Suppose that W is a finite, unitary, reflection group acting on the complex vector space V and X is a subspace of V. Define N to be the setwise stabilizer of X in W, Z to be the pointwise stabilizer, and C=N/Z. Then restriction defines a homomorphism from the algebra of W-invariant polynomial functions on V to the algebra of C-invariant functions on X. In this note we consider the special case when W is a Coxeter group, V is the complexified reflection representation of W, and X is in the lattice of the arrangement of W, and give a simple, combinatorial characterization of when the restriction mapping is surjective in terms of the exponents of W and C. As an application of our result, in the case when W is the Weyl group of a semisimple, complex Lie algebra, we complete a calculation begun by Richardson in 1987 and obtain a simple combinatorial characterization of regular decomposition classes whose closure is a normal variety.

We compare the cohomology of (parabolic) Hitchin fibers for Langlands dual groups G and G∨. The comparison theorem fits in the framework of the global Springer theory developed by the author. We prove that the stable parts of the parabolic Hitchin complexes for Langlands dual group are naturally isomorphic after passing to the associated graded of the perverse filtration. Moreover, this isomorphism intertwines the global Springer action on one hand and Chern class action on the other. Our result is inspired by the mirror symmetric viewpoint of geometric Langlands duality. Compared to the pioneer work in this subject by T. Hausel and M. Thaddeus, R. Donagi and T. Pantev, and N. Hitchin, our result is valid for more general singular fibers. The proof relies on a variant of Ngô’s support theorem, which is a key point in the proof of the Fundamental Lemma.

The normal residual finiteness growth of a group quantifies how well approximated the group is by its finite quotients. We show that any S-arithmetic subgroup of a higher rank Chevalley group G has normal residual finiteness growth ndim (G).

We devise a fairly general sufficient condition ensuring that the endomorphism monoid of a countably infinite ultrahomogeneous structure (i.e. a Fraïssé limit) embeds all countable semigroups. This approach not only provides us with a framework unifying the previous scattered results in this vein, but actually yields new applications for endomorphism monoids of the (rational) Urysohn space and the countable universal ultrahomogeneous semilattice.

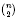Non-degenerate monoids of skew type are considered. This is a class of monoids S defined by n generators and quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FMn. of rank n the set of normal forms of elements of S is a regular language in FMn. As one of the key ingredients of the proof, it is shown that an identity of the form xN yN = yN xN holds in S. The latter is derived via an investigation of the structure of S viewed as a semigroup of matrices over a field. It also follows that the semigroup algebra K[S] is a finite module over a finitely generated commutative subalgebra of the form K[A] for a submonoid A of S.

Let G be a finite group. A subset X of G is a set of pairwise noncommuting elements if any two distinct elements of X do not commute. In this paper we determine the maximum size of these subsets in any finite nonabelian metacyclic p-group for an odd prime p.

We consider finite groups in which, for all primes p, the p-part of the length of any conjugacy class is trivial or fixed. We obtain a full description in the case in which for each prime divisor p of the order of the group there exists a noncentral conjugacy class of p-power size.

In Cossey and Stonehewer [‘On the rarity of quasinormal subgroups’, Rend. Semin. Mat. Univ. Padova125 (2011), 81–105] it is shown that for any odd prime p and integer n≥3, there is a finite p-group G of exponent pn containing a quasinormal subgroup H of exponent pn−1 such that the nontrivial quasinormal subgroups of G lying in H can have exponent only p, pn−1 or, when n≥4 , pn−2. Thus large sections of these groups are devoid of quasinormal subgroups. The authors ask in that paper if there is a nontrivial subgroup-theoretic property 𝔛 of finite p-groups such that (i) 𝔛 is invariant under subgroup lattice isomorphisms and (ii) every chain of 𝔛-subgroups of a finite p-group can be refined to a composition series of 𝔛-subgroups. Failing this, can such a chain always be refined to a series of 𝔛-subgroups in which the intervals between adjacent terms are restricted in some significant way? The present work embarks upon this quest.

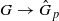Assume that G is a solvable group whose elementary abelian sections are all finite. Suppose, further, that p is a prime such that G fails to contain any subgroups isomorphic to Cp∞. We show that if G is nilpotent, then the pro-p completion map induces an isomorphism 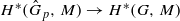for any discrete 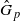-module 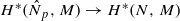M of finite p-power order. For the general case, we prove that G contains a normal subgroup N of finite index such that the map is an isomorphism for any discrete 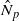-module M of finite p-power order. Moreover, if G lacks any Cp∞-sections, the subgroup N enjoys some additional special properties with respect to its pro-p topology.

Lattices of radicals have been extensively studied, for example in the class of associative rings, leading to some interesting results. In this paper we investigate the lattice L of all radicals in the class of all finite groups. We also consider some of its important sublattices. In particular, we prove that the lattice L is closed to being modular, the lattice Lh of all hereditary radicals is a Boolean algebra, and there exists a natural, useful projection of the lattice L onto Lh.

Let X be any set and P(X) the set of all partial transformations defined on X, that is, all functions α:A→B where A,B are subsets of X. Then P(X) is a semigroup under composition. Let Y be a subset of X. Recently, Fernandes and Sanwong defined PT(X,Y )={α∈P(X):Xα⊆Y } and defined I(X,Y )to be the set of all injective transformations in PT(X,Y ) . Hence PT(X,Y )and I(X,Y )are subsemigroups of P(X) . In this paper, we study properties of the so-called natural partial order ≤ on PT(X,Y )and I(X,Y )in terms of domains, images and kernels, compare ≤ with the subset order, characterise the meet and join of these two orders, then find elements of PT(X,Y )and I(X,Y )which are compatible. Also, the minimal and maximal elements are described.

Groups having exactly one normaliser are well known. They are the Dedekind groups. All finite groups having exactly two normalisers were classified by Pérez-Ramos [‘Groups with two normalizers’, Arch. Math.50 (1988), 199–203], and Camp-Mora [‘Locally finite groups with two normalizers’, Comm. Algebra28 (2000), 5475–5480] generalised that result to locally finite groups. Then Tota [‘Groups with a finite number of normalizer subgroups’, Comm. Algebra32 (2004), 4667–4674] investigated properties (such as solubility) of arbitrary groups with two, three and four normalisers. In this paper we prove that every finite group with at most 20 normalisers is soluble. Also we characterise all nonabelian simple (not necessarily finite) groups with at most 57 normalisers.

We consider the class of solvable groups in which all subnormal subgroups have subnormal normalizers, a class containing many well-known classes of solvable groups. Groups of this class have Fitting length three at most; some other information connected with the Fitting series is given.

It is well known that all saturated formations of finite soluble groups are locally defined and, except for the trivial formation, have many different local definitions. I show that for Lie and Leibniz algebras over a field of characteristic 0, the formations of all nilpotent algebras and of all soluble algebras are the only locally defined formations and the latter has many local definitions. Over a field of nonzero characteristic, a saturated formation of soluble Lie algebras has at most one local definition, but a locally defined saturated formation of soluble Leibniz algebras other than that of nilpotent algebras has more than one local definition.

In this paper, solubility of groups factorised as a product of two subgroups which are connected by certain permutability properties is studied.

We consider the wreath product of two permutation groups G≤Sym Γ and H≤Sym Δ as a permutation group acting on the set Π of functions from Δ to Γ. Such groups play an important role in the O’Nan–Scott theory of permutation groups and they also arise as automorphism groups of graph products and codes. Let X be a subgroup of Sym Γ≀Sym Δ. Our main result is that, in a suitable conjugate of X, the subgroup of SymΓ induced by a stabiliser of a coordinate δ∈Δ only depends on the orbit of δ under the induced action of X on Δ. Hence, if X is transitive on Δ, then X can be embedded into the wreath product of the permutation group induced by the stabiliser Xδ on Γ and the permutation group induced by X on Δ. We use this result to describe the case where X is intransitive on Δ and offer an application to error-correcting codes in Hamming graphs.

Suppose G is a p-solvable group, where p is odd. We explore the connection between lifts of Brauer characters of G and certain local objects in G, called vertex pairs. We show that if χ is a lift, then the vertex pairs of χ form a single conjugacy class. We use this to prove a sufficient condition for a given pair to be a vertex pair of a lift and to study the behaviour of lifts with respect to normal subgroups.

This paper studies two new kinds of affine Springer fibres that are adapted to the root valuation strata of Goresky–Kottwitz–MacPherson. In addition it develops various linear versions of Katz's Hodge–Newton decomposition.