Refine listing
Actions for selected content:
1959 results in 20xxx
Retracts of trees and free left adequate semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 17 August 2011, pp. 731-747
-
- Article
-
- You have access
- Export citation
TOPOLOGY OF THE REPRESENTATION VARIETIES WITH BOREL MOLD FOR UNSTABLE CASES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 11 October 2011, pp. 55-87
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Searching for small simple automorphic loops
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 200-213
-
- Article
-
- You have access
- Export citation
Computing character tables of groups of type M.G.A
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 173-178
-
- Article
-
- You have access
- Export citation
GEOMETRIC STRUCTURE IN THE TEMPERED DUAL OF SLℓ(F): TORAL CASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 425-432
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Actions of higher-rank lattices on free groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 1573-1580
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
THE CLASSIFICATION OF SOME MODULAR FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 July 2011, pp. 11-18
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ON B(5,k) GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 13 July 2011, pp. 393-407
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Factorization of the canonical bases for higher-level Fock spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 20 June 2011, pp. 23-51
-
- Article
-
- You have access
- Export citation
Symmetric presentations of Coxeter groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 669-683
-
- Article
-
- You have access
- Export citation
Idempotent-generated semigroups and pseudovarieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 545-568
-
- Article
-
- You have access
- Export citation
A NOTE ON NIELSEN EQUIVALENCE IN FINITELY GENERATED ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 127-136
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Alternating units as free factors in the group of units of integral group rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 695-709
-
- Article
-
- You have access
- Export citation
Characters and growth of admissible representations of reductive p-adic groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 June 2011, pp. 289-331
- Print publication:
- April 2012
-
- Article
- Export citation
ON VERBAL SUBGROUPS IN RESIDUALLY FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 10 June 2011, pp. 159-170
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
PRESENTATIONS OF INVERSE SEMIGROUPS, THEIR KERNELS AND EXTENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 08 July 2011, pp. 289-316
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Gaudin subalgebras and stable rational curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1463-1478
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Module structure on Lie powers and natural coalgebra-split sub-Hopf algebras of tensor algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 04 April 2011, pp. 467-504
-
- Article
-
- You have access
- Export citation
ON NONNILPOTENT SUBSETS IN GENERAL LINEAR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 369-375
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
EXOTIC LEFT-ORDERINGS OF THE FREE GROUPS FROM THE DEHORNOY ORDERING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 103-110
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
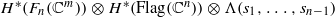 are isomorphic as algebras. Here the degree of
are isomorphic as algebras. Here the degree of  and
and  . They correspond to
. They correspond to  and
and  -module structures. We establish that the transition matrices relating these two bases are unitriangular with coefficients in ℕ[
-module structures. We establish that the transition matrices relating these two bases are unitriangular with coefficients in ℕ[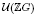 , the group of units of ℤ
, the group of units of ℤ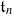 . We show that Gaudin subalgebras form a variety isomorphic to the moduli space
. We show that Gaudin subalgebras form a variety isomorphic to the moduli space 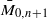 of stable curves of genus zero with
of stable curves of genus zero with 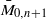 in a Grassmannian of (
in a Grassmannian of (