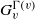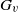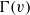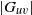Refine listing
Actions for selected content:
1959 results in 20xxx
ON THE ORDER OF ARC-STABILISERS IN ARC-TRANSITIVE GRAPHS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 441-447
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Computing Hall subgroups of finite groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 205-218
-
- Article
-
- You have access
- Export citation
The Brauer characters of the sporadic simple Harada–Norton group and its automorphism group in characteristics 2 and 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 257-280
-
- Article
-
- You have access
- Export citation
ALGORITHMS TO IDENTIFY ABUNDANT p-SINGULAR ELEMENTS IN FINITE CLASSICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 06 August 2012, pp. 50-63
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
PyCox: computing with (finite) Coxeter groups and Iwahori–Hecke algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 231-256
-
- Article
-
- You have access
- Export citation
Twisted gamma filtration of a linear algebraic group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1645-1654
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Quivers of monoids with basic algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1516-1560
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
FINITELY GENERATED SOLUBLE GROUPS WITH A CONDITION ON INFINITE SUBSETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 13 June 2012, pp. 152-157
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
GENERATING SYSTEMS OF SUBGROUPS IN SU(2, 1)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 346-352
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
ON THE VARIETY GENERATED BY THE MONOID OF TRIANGULAR 2×2 MATRICES OVER A TWO-ELEMENT FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 28 May 2012, pp. 64-77
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
NATURAL PARTIAL ORDER IN SEMIGROUPS OF TRANSFORMATIONS WITH INVARIANT SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 May 2012, pp. 94-107
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
ON WEAKLY s-PERMUTABLY EMBEDDED SUBGROUPS OF FINITE GROUPS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 21 May 2012, pp. 41-49
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
FINITE REGULAR BANDS ARE FINITELY RELATED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1-9
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
Condensation of homomorphism spaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 140-157
-
- Article
-
- You have access
- Export citation
Groups acting simply transitively on vertex sets of hyperbolic triangular buildings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 101-112
-
- Article
-
- You have access
- Export citation
On the centre of the cyclotomic Hecke algebra of G(m, 1, 2)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 497-506
-
- Article
-
- You have access
- Export citation
c-SECTIONS, SOLVABILITY AND LARGE SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 03 April 2012, pp. 291-302
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Testing commutativity of a group and the power of randomization
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 38-43
-
- Article
-
- You have access
- Export citation
A NOTE ON AUTOMORPHISMS OF FINITE p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 30 March 2012, pp. 24-26
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
ON TORSION OF CLASS GROUPS OF CM TORI
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 28 March 2012, pp. 305-318
- Print publication:
- July 2012
-
- Article
- Export citation