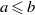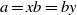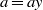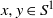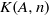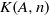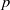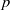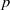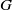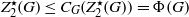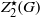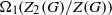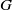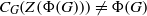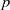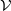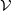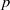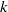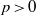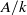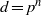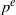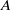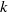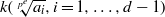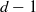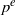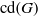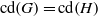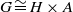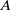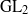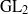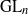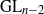Refine listing
Actions for selected content:
1959 results in 20xxx
Shifted generic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1765-1788
- Print publication:
- October 2013
-
- Article
- Export citation
REGULAR CONGRUENCES ON AN IDEMPOTENT-REGULAR-SURJECTIVE SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 190-196
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
PROFINITE GROUPS WITH FINITE VIRTUAL LENGTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 343-355
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
PRIMITIVE SUBGROUPS AND PST-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 373-378
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
PRIMITIVE PERMUTATION GROUPS CONTAINING A CYCLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 159-165
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
CONCISENESS OF COPRIME COMMUTATORS IN FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 252-258
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Unipotent differential algebraic groups as parameterized differential Galois groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 671-700
- Print publication:
- October 2014
-
- Article
- Export citation
Cohomological finiteness properties of the Brin–Thompson–Higman groups 2V and 3V
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 777-804
-
- Article
-
- You have access
- Export citation
Fusion systems and group actions with abelian isotropy subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 873-886
-
- Article
-
- You have access
- Export citation
Intersecting families in classical Coxeter groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 887-908
-
- Article
-
- You have access
- Export citation
THE NATURAL PARTIAL ORDER ON SOME TRANSFORMATION SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 279-292
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ON CONJUGACY OF SUPPLEMENTS OF NORMAL SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 293-299
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
AN EXPLICIT DESCRIPTION OF THE SIMPLICIAL GROUP
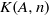 $K(A, n)$
$K(A, n)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 133-144
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
ON NONINNER AUTOMORPHISMS OF FINITE NONABELIAN
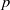 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 June 2013, pp. 202-209
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
CHARACTERIZING SOME COMPLETELY REGULAR SEMIGROUPS BY THEIR SUBSEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 397-416
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
MINIMAL VOLUME OF COMPLETE UNIFORM VISIBILITY MANIFOLDS WITH FINITE VOLUME
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 375-384
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
On the symbol length of
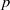 $p$-algebras
$p$-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 22 May 2013, pp. 1353-1363
- Print publication:
- August 2013
-
- Article
- Export citation
A SOLVABILITY CRITERION FOR FINITE LOOPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 30 April 2013, pp. 92-96
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON HUPPERT’S CONJECTURE FOR THE CONWAY AND FISCHER FAMILIES OF SPORADIC SIMPLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 11 April 2013, pp. 289-303
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
TILING BRANCHING MULTIPLICITY SPACES WITH GL
 ${}_{2} $ PATTERN BLOCKS
${}_{2} $ PATTERN BLOCKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 362-374
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation

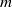
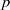
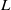
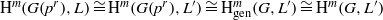
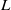
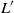
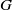
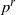
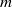
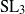
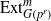
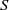
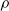
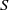
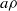
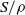
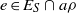
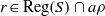
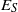
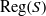
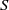
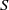
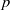
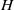
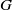
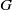

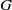
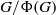
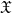
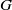
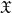
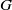
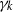
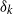
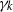
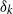
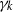
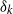
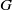
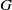
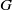
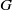

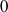
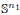 × … ×
× … × 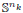 for some positive integers
for some positive integers