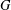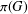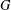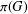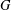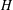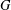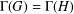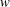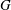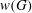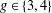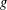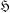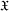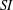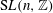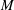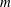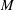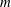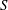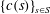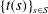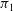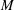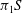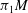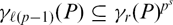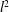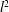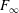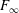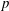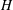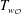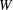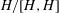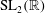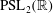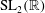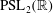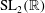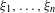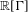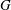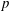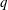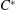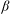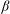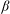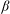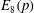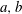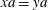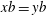Refine listing
Actions for selected content:
1959 results in 20xxx
ON THE PRIME GRAPH OF SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 227-240
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Computing symmetry groups of polyhedra
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 October 2014, pp. 565-581
-
- Article
-
- You have access
- Export citation
WORDS AND PRONILPOTENT SUBGROUPS IN PROFINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 29 September 2014, pp. 343-364
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
FINITE 3-GEODESIC TRANSITIVE BUT NOT 3-ARC TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 September 2014, pp. 183-190
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
CONDITIONS FOR A SCHUNCK CLASS TO BE A FORMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 69-75
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
ON SI-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 92-103
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Discrete automorphism groups of convex cones of finite type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 1939-1962
- Print publication:
- November 2014
-
- Article
- Export citation
THE CATENARY AND TAME DEGREES ON A NUMERICAL MONOID ARE EVENTUALLY PERIODIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 289-300
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Separability of embedded surfaces in 3-manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1623-1630
- Print publication:
- September 2014
-
- Article
- Export citation
A BOUND ON THE p-LENGTH OF P-SOLVABLE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 26 August 2014, pp. 167-171
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
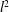 ${l}^{2}$-invisibility and a class of local similarity groups
${l}^{2}$-invisibility and a class of local similarity groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 19 August 2014, pp. 1742-1754
- Print publication:
- October 2014
-
- Article
- Export citation
Minimal length elements of extended affine Weyl groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 19 August 2014, pp. 1903-1927
- Print publication:
- November 2014
-
- Article
- Export citation
The constructive membership problem for discrete free subgroups of rank 2 of
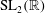 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{SL}_2(\mathbb{R})$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{SL}_2(\mathbb{R})$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 345-359
-
- Article
-
- You have access
- Export citation
Subexponential class group and unit group computation in large degree number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 385-403
-
- Article
-
- You have access
- Export citation
NONCOMMUTATIVE REAL ALGEBRAIC GEOMETRY OF KAZHDAN’S PROPERTY (T)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 30 July 2014, pp. 85-90
- Print publication:
- January 2016
-
- Article
- Export citation
NONORTHOGONAL GEOMETRIC REALIZATIONS OF COXETER GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 180-211
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
SOLVABILITY OF FINITE GROUPS WITH FOUR CONJUGACY CLASS SIZES OF CERTAIN ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 21 July 2014, pp. 250-256
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
TOPOLOGICAL FULL GROUPS OF
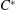 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM 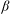 $\beta $-EXPANSIONS
$\beta $-EXPANSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 257-287
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Rational rigidity for
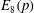 ${E}_{8}(p)$
${E}_{8}(p)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1679-1702
- Print publication:
- October 2014
-
- Article
- Export citation
ON WEAKLY AMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 404-417
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation