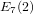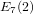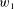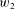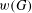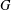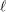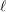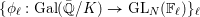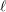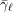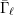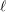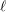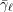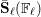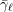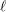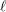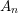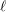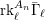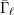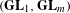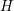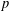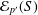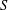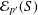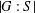Refine listing
Actions for selected content:
1959 results in 20xxx
The maximal subgroups of
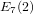 $E_{7}(2)$
$E_{7}(2)$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 323-371
-
- Article
-
- You have access
- Export citation
 $\wedge$-TRANSITIVE DIGRAPHS PRESERVING A CARTESIAN DECOMPOSITION
$\wedge$-TRANSITIVE DIGRAPHS PRESERVING A CARTESIAN DECOMPOSITION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 31 March 2015, pp. 85-107
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
A REFINED WARING PROBLEM FOR FINITE SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 17 March 2015, e6
-
- Article
-
- You have access
- Open access
- Export citation
ON GROUPS PRESENTED BY MONADIC REWRITING SYSTEMS WITH GENERATORS OF FINITE ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 426-434
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
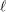 $\ell$-independence for compatible systems of (mod
$\ell$-independence for compatible systems of (mod 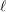 $\ell$) representations
$\ell$) representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 02 March 2015, pp. 1215-1241
- Print publication:
- July 2015
-
- Article
- Export citation
Projective geometry in characteristic one and the epicyclic category
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 95-132
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Endoscopie et conjecture locale raffinée de Gan–Gross–Prasad pour les groupes unitaires
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 18 February 2015, pp. 1309-1371
- Print publication:
- July 2015
-
- Article
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation
Spherical subgroups in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 13 February 2015, pp. 1288-1308
- Print publication:
- July 2015
-
- Article
- Export citation
A Numerical Lower Bound for the Spectral Radius of Random Walks on Surface Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 January 2015, pp. 838-856
-
- Article
- Export citation
THE NUMBER OF PROFINITE GROUPS WITH A SPECIFIED SYLOW SUBGROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 19 January 2015, pp. 108-127
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
‘COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 12 January 2015, pp. 351-352
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
McCammond’s normal forms for free aperiodic semigroups revisited
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 January 2015, pp. 130-147
-
- Article
-
- You have access
- Export citation
Finite basis problem for semigroups of order six
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 January 2015, pp. 1-129
-
- Article
-
- You have access
- Export citation
Coherent presentations of Artin monoids
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 957-998
- Print publication:
- May 2015
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE BRANCH LOCI OF NON-ORIENTABLE UNBORDERED KLEIN SURFACES OF LOW GENUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 211-230
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
LINEAR AND PROJECTIVE BOUNDARY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 591-632
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
COVERS FOR S-ACTS AND CONDITION (A) FOR A MONOID S
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 19 December 2014, pp. 323-341
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
STRONGLY INVARIANT SUBGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 431-443
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
COCOMPACT LATTICES ON Ãn BUILDINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 241-262
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation