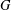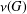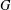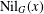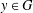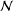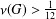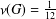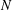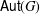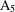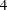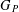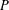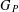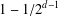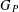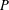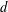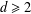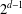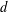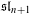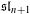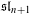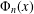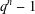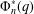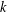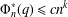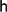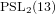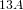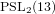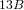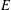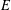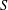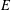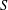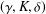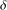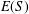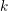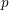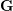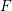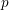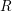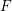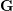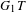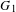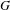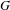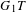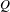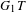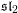Refine listing
Actions for selected content:
1959 results in 20xxx
Bounding the Diameter of the Brauer Graph of a Block of a Solvable Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 591-603
-
- Article
- Export citation
CoxIter – Computing invariants of hyperbolic Coxeter groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 754-773
-
- Article
-
- You have access
- Export citation
Geodesics in Trees of Hyperbolic and Relatively Hyperbolic Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 701-740
-
- Article
- Export citation
ON THE PROBABILITY OF GENERATING NILPOTENT SUBGROUPS IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 447-453
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 241-251
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
GROUPS OF INFINITE RANK WITH NORMALITY CONDITIONS ON SUBGROUPS WITH SMALL NORMAL CLOSURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 48-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A SUFFICIENT CONDITION UNDER WHICH A SEMIGROUP IS NONFINITELY BASED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 454-466
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 238-247
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
FINITELY CONSTRAINED GROUPS OF MAXIMAL HAUSDORFF DIMENSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 108-123
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
DEMAZURE MODULES OF LEVEL TWO AND PRIME REPRESENTATIONS OF QUANTUM AFFINE
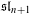 $\mathfrak{sl}_{n+1}$
$\mathfrak{sl}_{n+1}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 09 November 2015, pp. 75-105
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
THE CONTRIBUTION OF L. G. KOVÁCS TO THE THEORY OF PERMUTATION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 05 November 2015, pp. 20-33
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
PRIMITIVE PRIME DIVISORS AND THE
 $\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
$\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2015, pp. 122-135
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
Every
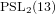 $\text{PSL}_{2}(13)$ in the Monster contains
$\text{PSL}_{2}(13)$ in the Monster contains 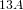 $13A$ -elements
$13A$ -elements
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 November 2015, pp. 667-674
-
- Article
-
- You have access
- Export citation
ON GENERALISED FC-GROUPS IN WHICH NORMALITY IS A TRANSITIVE RELATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 29 October 2015, pp. 192-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
COMPLETE LATTICE HOMOMORPHISM OF STRONGLY REGULAR CONGRUENCES ON
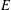 $E$-INVERSIVE SEMIGROUPS
$E$-INVERSIVE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 199-215
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
The pro-
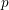 $p$-Iwahori Hecke algebra of a reductive
$p$-Iwahori Hecke algebra of a reductive 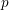 $p$-adic group I
$p$-adic group I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 23 October 2015, pp. 693-753
- Print publication:
- April 2016
-
- Article
- Export citation
‘ON SETS OF PP-GENERATORS OF FINITE GROUPS’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 05 October 2015, pp. 350-352
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
THE LOEWY STRUCTURE OF
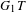 $G_{1}T$ -VERMA MODULES OFSINGULAR HIGHEST WEIGHTS
$G_{1}T$ -VERMA MODULES OFSINGULAR HIGHEST WEIGHTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 4 / September 2017
- Published online by Cambridge University Press:
- 02 October 2015, pp. 887-898
- Print publication:
- September 2017
-
- Article
- Export citation
The two-color Soergel calculus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 22 September 2015, pp. 327-398
- Print publication:
- February 2016
-
- Article
- Export citation