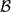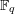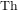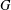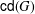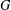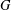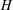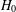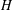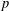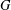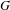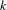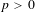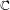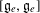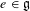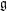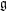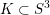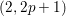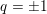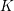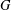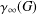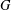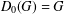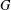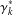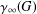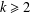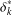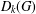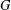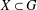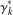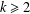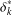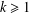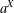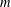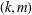Refine listing
Actions for selected content:
1959 results in 20xxx
Finite Groups and Lie Rings with an Automorphism of Order 2n
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 391-412
-
- Article
- Export citation
Free Monoids are Coherent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 127-131
-
- Article
- Export citation
ABELIAN AND METABELIAN QUOTIENT GROUPS OF SURFACE BRAID GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 119-142
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
LOCAL REPRESENTATIONS OF THE LOOP BRAID GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 359-378
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
EMBEDDING IN A FINITE 2-GENERATOR SEMIGROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 61-75
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
EQUIVARIANT COMPRESSION OF CERTAIN DIRECT LIMIT GROUPS AND AMALGAMATED FREE PRODUCTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 739-752
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
A NOTE ON THE
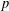 $p$ -SUPERSOLUBILITY OF FINITE GROUPS
$p$ -SUPERSOLUBILITY OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 03 June 2016, pp. 431-436
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Shintani descent for algebraic groups and almost characters of unipotent groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 1697-1724
- Print publication:
- August 2016
-
- Article
- Export citation
Finding 47:23 in the Baby Monster
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 229-234
-
- Article
-
- You have access
- Export citation
GROUPS WITH THE SAME CHARACTER DEGREES AS SPORADIC ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 254-265
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
On a Class of Automaton Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 31-38
-
- Article
- Export citation
REALIZABILITY PROBLEM FOR COMMUTING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 335-355
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
L. G. KOVÁCS AND LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 55-62
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
COCHAIN SEQUENCES AND THE QUILLEN CATEGORY OF A COCLASS FAMILY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 185-204
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON GEHRING–MARTIN–TAN GROUPS WITH AN ELLIPTIC GENERATOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 326-336
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SOLVABLE LIE GROUPS DEFINABLE IN O-MINIMAL THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 28 April 2016, pp. 441-452
- Print publication:
- April 2018
-
- Article
- Export citation
RIGID ORBITS AND SHEETS IN REDUCTIVE LIE ALGEBRAS OVER FIELDS OF PRIME CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 04 April 2016, pp. 583-613
- Print publication:
- June 2018
-
- Article
- Export citation
Double affine Hecke algebras and generalized Jones polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1333-1384
- Print publication:
- July 2016
-
- Article
- Export citation
Numerical semigroups with a given set of pseudo-Frobenius numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 186-205
-
- Article
-
- You have access
- Export citation
BOUNDING THE ORDER OF THE NILPOTENT RESIDUAL OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 273-277
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
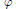 of order 2
of order 2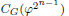 of the involution
of the involution 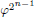 is nilpotent of class
is nilpotent of class 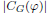 ) be the number of fixed points of
) be the number of fixed points of