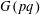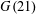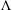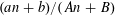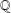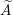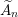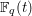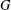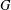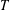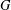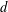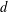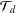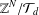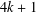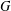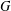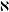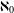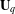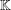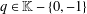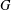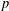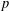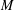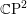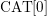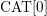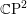Refine listing
Actions for selected content:
1959 results in 20xxx
Stable vectors in Moy–Prasad filtrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 358-372
- Print publication:
- February 2017
-
- Article
- Export citation
Rings of Polynomials With Artinian Coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 947-954
-
- Article
- Export citation
On the Universal SL2-Representation Rings of Free Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 973-1001
-
- Article
- Export citation
LOCALLY ANALYTIC REPRESENTATIONS OF
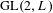 $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF
$\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 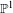 $\mathbb{P}^{1}$
$\mathbb{P}^{1}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 January 2017, pp. 125-187
- Print publication:
- January 2019
-
- Article
- Export citation
On the Asphericity of a Family of Positive Relative Group Presentations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 545-564
-
- Article
- Export citation
Corrigendum: Connected components of affine Deligne–Lusztig varieties in mixed characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 218-222
- Print publication:
- January 2017
-
- Article
-
- You have access
- HTML
- Export citation
AN EXPLICIT DIAGONAL RESOLUTION FOR A NON-ABELIAN METACYCLIC GROUP
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 March 2017, pp. 499-517
- Print publication:
- 2017
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
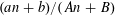 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
- Print publication:
- 2017
-
- Article
- Export citation
SYMMETRIC CROSSCAP NUMBER OF GROUPS OF ORDER LESS THAN OR EQUAL TO 63
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 145-156
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM, FIELDS OF VALUES FOR CHARACTERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 December 2016, pp. 37-43
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
On Groups with Slow Intersection Growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 14 November 2016, pp. 387-390
-
- Article
- Export citation
Affine Weyl group multiple Dirichlet series: type
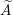 $\widetilde{A}$
$\widetilde{A}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2503-2523
- Print publication:
- December 2016
-
- Article
- Export citation
A NOTE ON GROUPS WHOSE PROPER LARGE SUBGROUPS HAVE A TRANSITIVE NORMALITY RELATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 38-47
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
SEMIPERMUTABILITY IN GENERALISED SOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 219-227
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
NILPOTENCY IN UNCOUNTABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 27 October 2016, pp. 59-69
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
SEMISIMPLICITY OF HECKE AND (WALLED) BRAUER ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1-44
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
SOME INFINITE PERMUTATION GROUPS AND RELATED FINITE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 136-149
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Ramification conjecture and Hirzebruch’s property of line arrangements
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 25 October 2016, pp. 2443-2460
- Print publication:
- December 2016
-
- Article
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
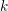
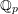
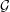
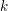
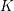
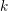
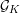
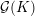
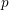
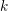
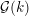
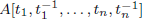 with coefficients in an Artinian ring
with coefficients in an Artinian ring 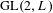
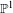
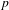

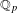
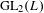
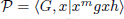 for
for