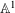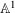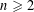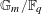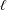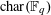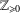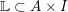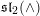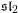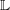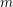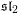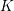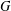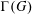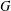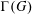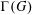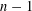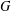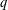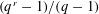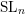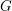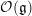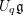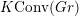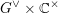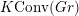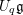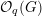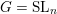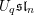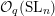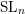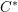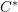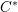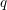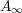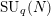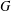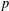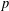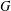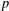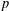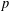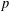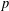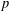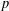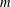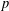Refine listing
Actions for selected content:
1959 results in 20xxx
VARIETIES OF LEFT RESTRICTION SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 29 January 2018, pp. 173-200
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
WEAK CAYLEY TABLE GROUPS OF SOME CRYSTALLOGRAPHIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 635-660
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WITH ENGEL SINKS OF BOUNDED RANK
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 695-701
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
RIGID LOCAL SYSTEMS ON
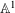 $\mathbb{A}^{1}$ WITH FINITE MONODROMY
$\mathbb{A}^{1}$ WITH FINITE MONODROMY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 785-846
- Print publication:
- 2018
-
- Article
- Export citation
INTEGRAL MONODROMY GROUPS OF KLOOSTERMAN SHEAVES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 652-678
- Print publication:
- 2018
-
- Article
- Export citation
CLASSIFICATION OF SPIN STRUCTURES ON FOUR-DIMENSIONAL ALMOST-FLAT MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 253-266
- Print publication:
- 2018
-
- Article
- Export citation
Commutativity preserving extensions of groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 20 December 2017, pp. 575-592
- Print publication:
- June 2018
-
- Article
- Export citation
REALISABLE SETS OF CATENARY DEGREES OF NUMERICAL MONOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 240-245
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Annular Khovanov homology and knotted Schur–Weyl representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 28 November 2017, pp. 459-502
- Print publication:
- March 2018
-
- Article
- Export citation
ALTERNATING AND SYMMETRIC GROUPS WITH EULERIAN GENERATING GRAPH
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 November 2017, e24
-
- Article
-
- You have access
- Open access
- Export citation
ON A THEOREM OF KANG AND LIU ON FACTORISED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 54-56
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
GENERATION OF SECOND MAXIMAL SUBGROUPS AND THE EXISTENCE OF SPECIAL PRIMES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 07 November 2017, e25
-
- Article
-
- You have access
- Open access
- Export citation
ON POWERS OF HALF-TWISTS IN M(0, 2n)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 333-338
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Quantum K-theoretic geometric Satake: the
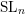 $\operatorname{SL}_{n}$ case
$\operatorname{SL}_{n}$ case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 275-327
- Print publication:
- February 2018
-
- Article
- Export citation
Howe–Moore type theorems for quantum groups and rigid
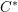 $C^{\ast }$ -tensor categories
$C^{\ast }$ -tensor categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 328-341
- Print publication:
- February 2018
-
- Article
- Export citation
DIAGRAM ALGEBRAS, DOMINANCE TRIANGULARITY AND SKEW CELL MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 13-36
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Homotopy linear algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 293-325
- Print publication:
- April 2018
-
- Article
- Export citation
GRAPH PRODUCTS AND THE ABSENCE OF PROPERTY (AR)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 274-288
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 215-217
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
CLASSIFICATION OF REFLECTION SUBGROUPS MINIMALLY CONTAINING
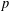 $p$ -SYLOW SUBGROUPS
$p$ -SYLOW SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 57-68
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation