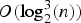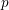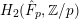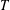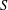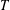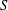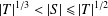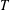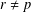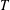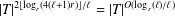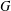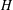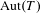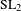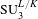Refine listing
Actions for selected content:
1959 results in 20xxx
ON
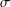 $\unicode[STIX]{x1D70E}$-QUASINORMAL SUBGROUPS OF FINITE GROUPS
$\unicode[STIX]{x1D70E}$-QUASINORMAL SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 413-420
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
PRESENTATIONS OF AFFINE KAC–MOODY GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 26 October 2018, e21
-
- Article
-
- You have access
- Open access
- Export citation
THE GEOMETRY OF BLUEPRINTS PART II: TITS–WEYL MODELS OF ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 October 2018, e20
-
- Article
-
- You have access
- Open access
- Export citation
On the First Zassenhaus Conjecture and Direct Products
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 15 October 2018, pp. 602-624
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Springer correspondence for the split symmetric pair in type
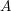 $A$
$A$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2403-2425
- Print publication:
- November 2018
-
- Article
- Export citation
COMPLEX OF RELATIVELY HYPERBOLIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 09 October 2018, pp. 657-672
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
CHARACTERIZING n-ISOCLINIC CLASSES OF CROSSED MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 08 October 2018, pp. 637-656
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Conditions for Sylow 2-subgroups of the Fixed Point Subgroup Implying Solubility
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 211-220
-
- Article
- Export citation
Low Growth Equational Complexity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 197-210
-
- Article
- Export citation
The HOMFLY-PT polynomials of sublinks and the Yokonuma–Hecke algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 18 September 2018, pp. 1269-1278
- Print publication:
- December 2018
-
- Article
- Export citation
GROUPS SATISFYING THE DOUBLE CHAIN CONDITION ON ABELIAN SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 September 2018, pp. 212-218
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On discrete homology of a free pro-
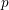 $p$-group
$p$-group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 07 September 2018, pp. 2195-2204
- Print publication:
- October 2018
-
- Article
- Export citation
Univariate and multivariate stochastic orderings of residual lifetimes of live components in sequential (𝑛-𝑟+ 1)-out-of-𝑛 systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 834-844
- Print publication:
- September 2018
-
- Article
- Export citation
ON THE SECOND-LARGEST SYLOW SUBGROUP OF A FINITE SIMPLE GROUP OF LIE TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 203-211
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
OVERGROUPS OF WEAK SECOND MAXIMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 83-88
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
PROJECTIVE CHARACTERS WITH PRIME POWER DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 78-82
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
LOCALLY COMPACT WREATH PRODUCTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 26-52
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
TEST MAP AND DISCRETENESS IN SL(2, ℍ)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 07 August 2018, pp. 523-533
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
CHABAUTY LIMITS OF SIMPLE GROUPS ACTING ON TREES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1093-1120
- Print publication:
- July 2020
-
- Article
- Export citation
CHABAUTY LIMITS OF ALGEBRAIC GROUPS ACTING ON TREES THE QUASI-SPLIT CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1031-1091
- Print publication:
- July 2020
-
- Article
- Export citation
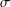























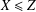

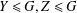




















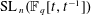
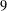
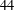
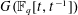
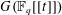
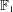

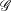
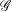
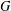
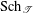
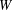
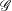
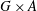
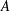
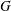
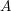





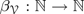
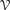 bounds the size of equation required to determine the membership of
bounds the size of equation required to determine the membership of 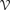 . Known examples of finitely generated varieties
. Known examples of finitely generated varieties 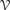 with unbounded equational complexity have growth in Ω(
with unbounded equational complexity have growth in Ω(