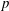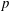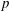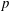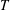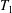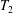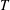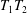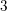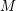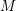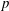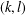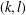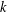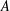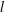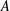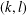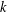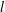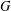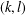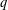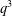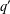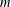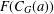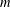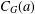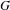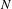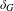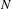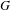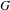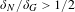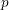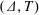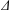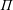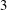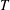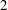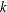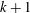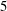Refine listing
Actions for selected content:
1959 results in 20xxx
Mixed Perverse Sheaves on Flag Varieties for Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1-55
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Growth of Homology of Centre-by-metabelian Pro-
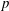 $p$ Groups
$p$ Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 203-224
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Merge Decompositions, Two-sided Krohn–Rhodes, and Aperiodic Pointlikes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 199-208
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Degrees of Regular Sequences With a Symmetric Group Action
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 557-578
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Profinite detection of 3-manifold decompositions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 246-259
- Print publication:
- February 2019
-
- Article
- Export citation
Casselman’s Basis of Iwahori Vectors and Kazhdan–Lusztig Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1351-1366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Galois theory for general systems of polynomial equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 229-245
- Print publication:
- February 2019
-
- Article
- Export citation
A problem of integer partitions and numerical semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 969-978
- Print publication:
- August 2019
-
- Article
- Export citation
Unitary and Symmetric Units of a Commutative Group Algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 641-654
-
- Article
- Export citation
THE MAXIMUM SIZE OF
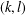 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
FITTING SUBGROUP AND NILPOTENT RESIDUAL OF FIXED POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 61-67
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A VON NEUMANN ALGEBRA CHARACTERIZATION OF PROPERTY (T) FOR GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 363-386
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
- Print publication:
- November 2020
-
- Article
- Export citation
Cogrowth for group actions with strongly contracting elements
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1738-1754
- Print publication:
- July 2020
-
- Article
- Export citation
Left Braces and the Quantum Yang–Baxter Equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 595-608
-
- Article
- Export citation
The Structure of Root Data and Smooth Regular Embeddings of Reductive Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 523-552
-
- Article
- Export citation
Fields of Definition for Representations of Associative Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 November 2018, pp. 291-304
-
- Article
- Export citation
Factorizations in Bounded Hereditary Noetherian Prime Rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 395-442
-
- Article
- Export citation
ON THE GALOIS STRUCTURE OF ARITHMETIC COHOMOLOGY I: COMPACTLY SUPPORTED
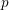 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 294-321
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Tits Triangles
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 November 2018, pp. 583-601
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation