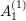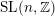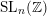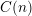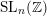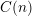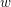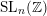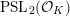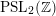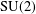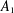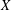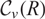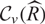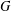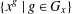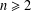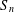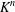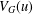Refine listing
Actions for selected content:
1959 results in 20xxx
Affine cluster monomials are generalized minors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 14 June 2019, pp. 1301-1326
- Print publication:
- July 2019
-
- Article
- Export citation
Words have bounded width in
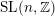 $\operatorname{SL}(n,\mathbb{Z})$
$\operatorname{SL}(n,\mathbb{Z})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1245-1258
- Print publication:
- July 2019
-
- Article
- Export citation
Renewal processes, population dynamics, and unimodular trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 339-357
- Print publication:
- June 2019
-
- Article
- Export citation
Martin boundaries of the duals of free unitary quantum groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 31 May 2019, pp. 1171-1193
- Print publication:
- June 2019
-
- Article
- Export citation
ON A PROBLEM OF PRAEGER AND SCHNEIDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 80-87
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Permutation groups containing a regular abelian subgroup: the tangled history of two mistakes of Burnside
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 613-633
- Print publication:
- May 2020
-
- Article
- Export citation
Robinson’s conjecture on heights of characters
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1098-1117
- Print publication:
- June 2019
-
- Article
- Export citation
Linear syzygies, hyperbolic Coxeter groups and regularity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1076-1097
- Print publication:
- June 2019
-
- Article
- Export citation
Local-global principles in circle packings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1118-1170
- Print publication:
- June 2019
-
- Article
- Export citation
EXCHANGE MOVES AND NONCONJUGATE BRAID REPRESENTATIVES OF KNOTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 20 May 2019, pp. 298-321
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
ON THE PROBABILITY DISTRIBUTION OF THE PRODUCT OF POWERS OF ELEMENTS IN COMPACT LIE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 440-445
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
JSJ DECOMPOSITIONS OF DOUBLES OF FREE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 02 May 2019, pp. 367-382
- Print publication:
- May 2020
-
- Article
-
- You have access
- Open access
- Export citation
AN IDENTITY OF PARABOLIC KAZHDAN–LUSZTIG POLYNOMIALS ARISING FROM SQUARE-IRREDUCIBLE MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 April 2019, pp. 81-93
- Print publication:
- February 2021
-
- Article
- Export citation
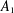 $A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
$A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 24 April 2019, e12
-
- Article
-
- You have access
- Open access
- Export citation
Embedding right-angled Artin groups into Brin–Thompson groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 23 April 2019, pp. 225-229
- Print publication:
- September 2020
-
- Article
- Export citation
Weak containment of measure-preserving group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 17 April 2019, pp. 2681-2733
- Print publication:
- October 2020
-
- Article
- Export citation
ON THE ARITHMETIC OF MORI MONOIDS AND DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 313-322
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
ON SUB-CLASS SIZES OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 402-411
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON THE DIMENSION OF PERMUTATION VECTOR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 April 2019, pp. 256-267
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation