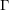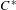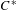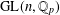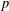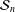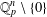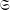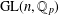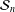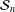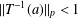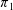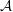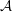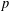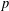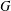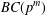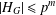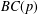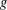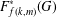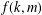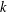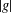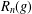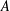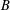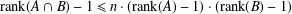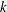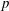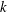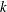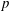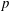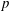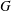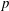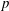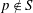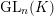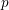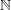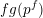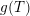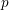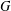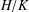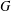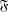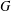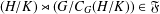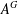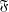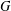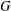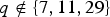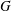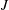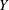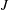Refine listing
Actions for selected content:
1959 results in 20xxx
Décomposition de Hodge pour l’homologie stable des groupes d’automorphismes des groupes libres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1794-1844
- Print publication:
- September 2019
-
- Article
- Export citation
On graph products of multipliers and the Haagerup property for
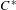 $C^{\ast }$-dynamical systems
$C^{\ast }$-dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 3188-3216
- Print publication:
- December 2020
-
- Article
- Export citation
On the residual and profinite closures of commensurated subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 30 July 2019, pp. 411-432
- Print publication:
- September 2020
-
- Article
- Export citation
DISTALITY OF CERTAIN ACTIONS ON
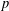 $p$-ADIC SPHERES
$p$-ADIC SPHERES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 250-261
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Bounded Depth Ascending HNN Extensions and
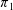 $\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity
$\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 22 July 2019, pp. 1529-1550
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
FINITE
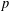 $p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
$p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 255-265
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
RIGHT ENGEL-TYPE SUBGROUPS AND LENGTH PARAMETERS OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 340-350
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
INTERSECTIONS OF SUBGROUPS IN VIRTUALLY FREE GROUPS AND VIRTUALLY FREE PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 266-271
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Retract Rationality and Algebraic Tori
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 173-186
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
The BNSR-invariants of the Houghton groups, concluded
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 15 July 2019, pp. 1-11
-
- Article
- Export citation
Kirillov’s orbit method and polynomiality of the faithful dimension of
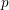 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 1618-1654
- Print publication:
- August 2019
-
- Article
- Export citation
ON A LATTICE CHARACTERISATION OF FINITE SOLUBLE PST-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 247-254
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Proof of the Brown–Erdős–Sós conjecture in groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 04 July 2019, pp. 323-333
- Print publication:
- September 2020
-
- Article
- Export citation
Coprime subdegrees of twisted wreath permutation groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 28 June 2019, pp. 1137-1162
-
- Article
- Export citation
CLASSIFICATION OF FINITE GROUPS VIA THEIR BREADTH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 June 2019, pp. 544-563
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Non-cocompact Group Actions and
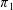 $\unicode[STIX]{x1D70B}_{1}$-Semistability at Infinity
$\unicode[STIX]{x1D70B}_{1}$-Semistability at Infinity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 26 June 2019, pp. 1275-1303
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Actions of skew braces and set-theoretic solutions of the reflection equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1089-1113
-
- Article
- Export citation
Recurrence of quadratic differentials for harmonic measure
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 25 June 2019, pp. 299-305
- Print publication:
- September 2020
-
- Article
- Export citation
The multistep homology of the simplex and representations of symmetric groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 20 June 2019, pp. 231-253
- Print publication:
- September 2020
-
- Article
- Export citation
ON THE RECOGNITION OF RIGHT-ANGLED ARTIN GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 19 June 2019, pp. 473-475
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation