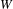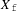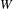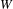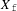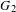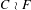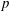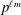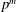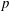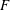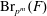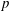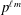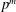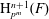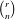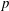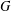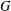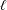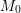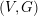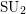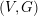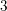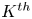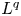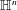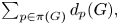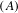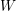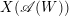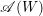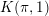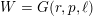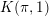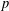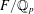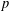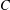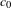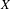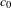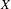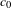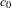Refine listing
Actions for selected content:
1959 results in 20xxx
Enumerating isoclinism classes of semi-extraspecial groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 24 February 2020, pp. 426-442
-
- Article
- Export citation
THE
 $q$-SCHUR ALGEBRAS AND
$q$-SCHUR ALGEBRAS AND  $q$-SCHUR DUALITIES OF FINITE TYPE
$q$-SCHUR DUALITIES OF FINITE TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 19 February 2020, pp. 129-160
- Print publication:
- January 2022
-
- Article
- Export citation
Simple groups and irreducible lattices in wreath products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1502-1513
- Print publication:
- May 2021
-
- Article
- Export citation
Amenable uniformly recurrent subgroups and lattice embeddings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1464-1501
- Print publication:
- May 2021
-
- Article
- Export citation
Essential Dimension, Symbol Length and
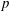 $p$-rank
$p$-rank
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 882-890
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
THE INTERSECTION MOTIVE OF THE MODULI STACK OF SHTUKAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 February 2020, e8
-
- Article
-
- You have access
- Open access
- Export citation
Symplectic quotients have symplectic singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 31 January 2020, pp. 613-646
- Print publication:
- March 2020
-
- Article
- Export citation
Dehn filling Dehn twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 January 2020, pp. 28-51
- Print publication:
- February 2021
-
- Article
- Export citation
LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 1931-1946
- Print publication:
- November 2021
-
- Article
- Export citation
Ideal Uniform Polyhedra in
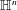 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 465-492
- Print publication:
- April 2021
-
- Article
- Export citation
CHARACTER LEVELS AND CHARACTER BOUNDS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 January 2020, e2
-
- Article
-
- You have access
- Open access
- Export citation
Bounding the maximal size of independent generating sets of finite groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 January 2020, pp. 133-150
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
A construction of subshifts and a class of semigroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 881-905
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
OPTIMAL LINE PACKINGS FROM FINITE GROUP ACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e6
-
- Article
-
- You have access
- Open access
- Export citation
On the
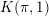 $K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
$K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 20 January 2020, pp. 526-532
- Print publication:
- March 2020
-
- Article
- Export citation
AXIOMATISABILITY OF THE CLASS OF MONOLITHIC GROUPS IN A VARIETY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 67-76
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF ADMISSIBLE SUPERSINGULAR REPRESENTATIONS OF
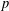 $p$-ADIC REDUCTIVE GROUPS
$p$-ADIC REDUCTIVE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 January 2020, e2
-
- Article
-
- You have access
- Open access
- Export citation
Revisiting Leighton’s theorem with the Haar measure
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 615-623
- Print publication:
- May 2021
-
- Article
- Export citation
A NEW COARSELY RIGID CLASS OF BANACH SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 1729-1747
- Print publication:
- September 2021
-
- Article
- Export citation
Moufang loops with nonnormal commutative centre
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 609-614
- Print publication:
- May 2021
-
- Article
- Export citation