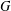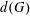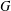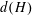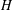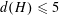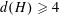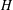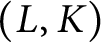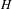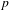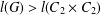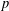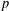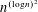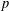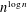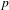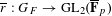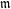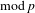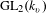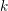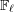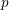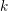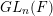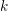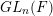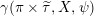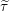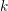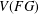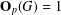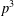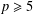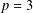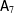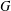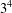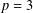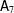Refine listing
Actions for selected content:
1959 results in 20xxx
GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e32
-
- Article
-
- You have access
- Open access
- Export citation
Positive definite functions and cut-off for discrete groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 22 June 2020, pp. 306-322
- Print publication:
- June 2021
-
- Article
- Export citation
Relative vertex asphericity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 June 2020, pp. 292-305
- Print publication:
- June 2021
-
- Article
- Export citation
Big mapping class groups and rigidity of the simple circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 03 June 2020, pp. 1961-1987
- Print publication:
- July 2021
-
- Article
- Export citation
Divergence, undistortion and Hölder continuous cocycle superrigidity for full shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 2274-2293
- Print publication:
- August 2021
-
- Article
- Export citation
HIGHER DEFORMATIONS OF LIE ALGEBRA REPRESENTATIONS II
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 232-255
- Print publication:
- December 2021
-
- Article
- Export citation
HOMOGENEOUS STRUCTURES WITH NONUNIVERSAL AUTOMORPHISM GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 817-827
- Print publication:
- June 2020
-
- Article
- Export citation
FIRST-ORDER RECOGNIZABILITY IN FINITE AND PSEUDOFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 852-867
- Print publication:
- June 2020
-
- Article
- Export citation
PROPERTIES OF FINITE GROUPS DETERMINED BY THE PRODUCT OF THEIR ELEMENT ORDERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 June 2020, pp. 88-95
- Print publication:
- February 2021
-
- Article
- Export citation
ENDOSCOPY FOR HECKE CATEGORIES, CHARACTER SHEAVES AND REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
BRANCH GROUPS, ORBIT GROWTH, AND SUBGROUP GROWTH TYPES FOR PRO-
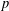 $p$ GROUPS
$p$ GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
RELATIVE COMPLETE REDUCIBILITY AND NORMALIZED SUBGROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e30
-
- Article
-
- You have access
- Open access
- Export citation
A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 21 May 2020, pp. 1153-1170
- Print publication:
- August 2021
-
- Article
- Export citation
DECOMPOSITION THEOREMS FOR AUTOMORPHISM GROUPS OF TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 104-112
- Print publication:
- February 2021
-
- Article
- Export citation
MULTIPLICITY ONE AT FULL CONGRUENCE LEVEL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 15 May 2020, pp. 637-658
- Print publication:
- March 2022
-
- Article
- Export citation
ISOTOPY AND HOMEOMORPHISM OF CLOSED SURFACE BRAIDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 297-306
- Print publication:
- May 2021
-
- Article
- Export citation
A NOTE ON CHAINS AND BOUNDING PAIRS OF DEHN TWISTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 133-138
- Print publication:
- January 2021
-
- Article
- Export citation
CHARACTERIZING THE MOD-
 $\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
$\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 119-135
- Print publication:
- December 2021
-
- Article
- Export citation
GROUP ALGEBRAS WHOSE UNIT GROUP IS LOCALLY NILPOTENT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 17-23
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A NOTE ON
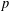 $p$-PARTS OF BRAUER CHARACTER DEGREES
$p$-PARTS OF BRAUER CHARACTER DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 06 May 2020, pp. 83-87
- Print publication:
- February 2021
-
- Article
- Export citation