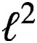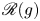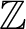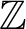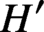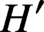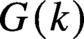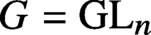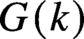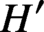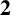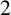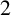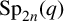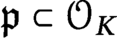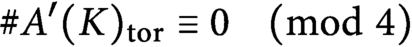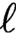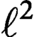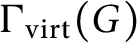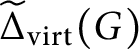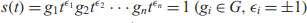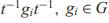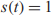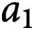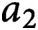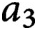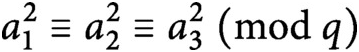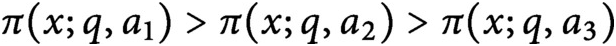Refine listing
Actions for selected content:
1959 results in 20xxx
Generic Newton points and the Newton poset in Iwahori-double cosets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e50
-
- Article
-
- You have access
- Open access
- Export citation
Profinite invariants of arithmetic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e54
-
- Article
-
- You have access
- Open access
- Export citation
Compact groups in which all elements have countable right Engel sinks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 1790-1814
- Print publication:
- December 2021
-
- Article
- Export citation
Boolean lattices in finite alternating and symmetric groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e55
-
- Article
-
- You have access
- Open access
- Export citation
Complete regularity of Ellis semigroups of
 $\mathbb{Z} $-actions
$\mathbb{Z} $-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3593-3609
- Print publication:
- December 2021
-
- Article
- Export citation
Semisimplification for subgroups of reductive algebraic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e43
-
- Article
-
- You have access
- Open access
- Export citation
THE INDUCTIVE BLOCKWISE ALPERIN WEIGHT CONDITION FOR TYPE
 ${\boldsymbol{\mathsf{C}}}$ AND THE PRIME
${\boldsymbol{\mathsf{C}}}$ AND THE PRIME 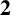 $\textbf{2}$
$\textbf{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 06 November 2020, pp. 1-20
- Print publication:
- August 2022
-
- Article
- Export citation
Bounds for finite semiprimitive permutation groups: order, base size, and minimal degree
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1071-1091
-
- Article
- Export citation
ON THE DIMENSION OF GROUPS THAT SATISFY CERTAIN CONDITIONS ON THEIR FINITE SUBGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 04 November 2020, pp. 45-50
- Print publication:
- January 2022
-
- Article
- Export citation
Topological flows for hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3474-3520
- Print publication:
- November 2021
-
- Article
- Export citation
Divisibility of torsion subgroups of abelian surfaces over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 28 October 2020, pp. 266-298
- Print publication:
- February 2022
-
- Article
- Export citation
COMPUTABILITY, ORDERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1588-1598
- Print publication:
- December 2020
-
- Article
- Export citation
The virtually generating graph of a profinite group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 808-819
- Print publication:
- December 2021
-
- Article
- Export citation
ON SOLVABILITY OF CERTAIN EQUATIONS OF ARBITRARY LENGTH OVER TORSION-FREE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 October 2020, pp. 651-659
- Print publication:
- September 2021
-
- Article
- Export citation
Variations on results on orders of products in finite groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 12 October 2020, pp. 1443-1449
- Print publication:
- October 2021
-
- Article
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
FURTHER REMARKS ON ELEMENTARY RADICALS AND ASSOCIATED FILTERS OF IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 08 October 2020, pp. 450-460
- Print publication:
- June 2021
-
- Article
- Export citation
CONNECTIVITY PROPERTIES OF MCKAY QUIVERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 182-194
- Print publication:
- April 2021
-
- Article
- Export citation
Arithmeticity of discrete subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2561-2590
- Print publication:
- September 2021
-
- Article
- Export citation
BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 461-474
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- Export citation