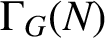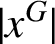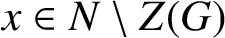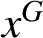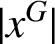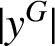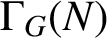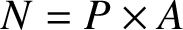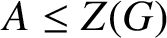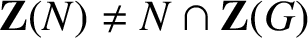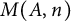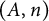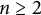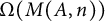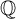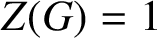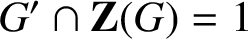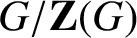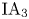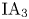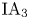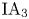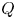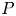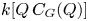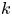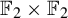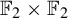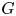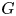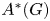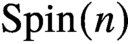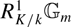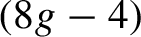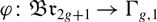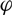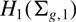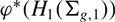Refine listing
Actions for selected content:
1959 results in 20xxx
ON THE REGULAR GRAPH RELATED TO THE G-CONJUGACY CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 101-105
- Print publication:
- February 2022
-
- Article
- Export citation
GROUPS WITH MANY PRONORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 75-86
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
On homotopy nilpotency of loop spaces of Moore spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 296-307
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING RESULTS OF MORGAN AND PARKER ABOUT COMMUTING GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 92-100
- Print publication:
- February 2022
-
- Article
- Export citation
On the low-dimensional cohomology groups of the IA-automorphism group of the free group of rank three
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 338-363
-
- Article
-
- You have access
- Open access
- Export citation
Dynamic asymptotic dimension for actions of virtually cyclic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 364-372
-
- Article
- Export citation
Brauer indecomposability of Scott modules with semidihedral vertex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 174-182
-
- Article
- Export citation
On sofic approximations of
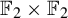 ${\mathbb F}_2\times {\mathbb F}_2$
${\mathbb F}_2\times {\mathbb F}_2$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2333-2351
- Print publication:
- July 2022
-
- Article
- Export citation
Automorphic vector bundles on the stack of G-zips
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 May 2021, e37
-
- Article
-
- You have access
- Open access
- Export citation
Infinitely presented permutation stable groups and invariant random subgroups of metabelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 30 April 2021, pp. 2028-2063
- Print publication:
- June 2022
-
- Article
- Export citation
Hopf-theoretic approach to motives of twisted flag varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 963-996
- Print publication:
- May 2021
-
- Article
- Export citation
Maximal indexes of flag varieties for spin groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 April 2021, e34
-
- Article
-
- You have access
- Open access
- Export citation
Explicit methods for the Hasse norm principle and applications to An and Sn extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 489-529
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
On the Finiteness length of some soluble linear groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1209-1243
- Print publication:
- October 2022
-
- Article
- Export citation
Uniconnected solutions to the Yang–Baxter equation arising from self-maps of groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 225-233
- Print publication:
- March 2022
-
- Article
- Export citation
Flexibility of measure-theoretic entropy of boundary maps associated to Fuchsian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 389-401
- Print publication:
- February 2022
-
- Article
- Export citation
BEING CAYLEY AUTOMATIC IS CLOSED UNDER TAKING WREATH PRODUCT WITH VIRTUALLY CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 13 April 2021, pp. 464-474
- Print publication:
- December 2021
-
- Article
- Export citation
INVARIANT SETS AND NORMAL SUBGROUPOIDS OF UNIVERSAL ÉTALE GROUPOIDS INDUCED BY CONGRUENCES OF INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 April 2021, pp. 99-118
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- Export citation
Lower central series, surface braid groups, surjections and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 373-399
- Print publication:
- March 2022
-
- Article
- Export citation
Braid groups, mapping class groups and their homology with twisted coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 249-266
- Print publication:
- March 2022
-
- Article
- Export citation