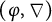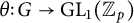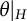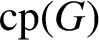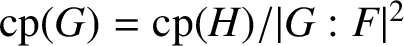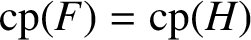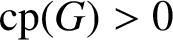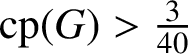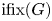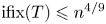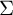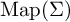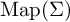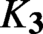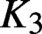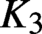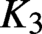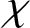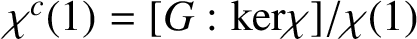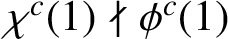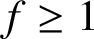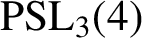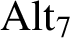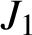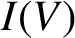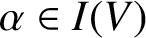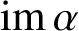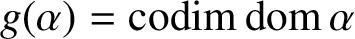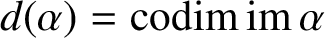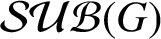Refine listing
Actions for selected content:
1959 results in 20xxx
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
Inverse K-Chevalley formulas for semi-infinite flag manifolds, I: minuscule weights in ADE type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 July 2021, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphisms and opposition in spherical buildings of exceptional type, I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 05 July 2021, pp. 1517-1578
- Print publication:
- December 2022
-
- Article
- Export citation
A group-theoretic generalization of the p-adic local monodromy theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 1450-1485
- Print publication:
- October 2022
-
- Article
- Export citation
Galois-theoretic features for 1-smooth pro-p groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 525-541
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMMUTING PROBABILITY OF COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 June 2021, pp. 87-91
- Print publication:
- February 2022
-
- Article
- Export citation
Monoidal abelian envelopes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 1584-1609
- Print publication:
- July 2021
-
- Article
- Export citation
ON GROUPS WHOSE SUBGROUPS ARE EITHER MODULAR OR CONTRANORMAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 286-295
- Print publication:
- April 2022
-
- Article
- Export citation
On class 2 quotients of linear groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 09 June 2021, pp. 590-593
-
- Article
- Export citation
SYMÉTRIES ET TRANSVEXIONS, PRINCIPALEMENT DANS LES GROUPES DE RANG DE MORLEY FINI SANS INVOLUTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 965-990
- Print publication:
- September 2021
-
- Article
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
On the involution fixity of simple groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 408-426
-
- Article
- Export citation
COMMUTATOR EQUATIONS IN FINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 320-335
- Print publication:
- May 2022
-
- Article
- Export citation
BIG MAPPING CLASS GROUPS WITH HYPERBOLIC ACTIONS: CLASSIFICATION AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 2173-2204
- Print publication:
- November 2022
-
- Article
- Export citation
Hyperbolic tessellations and generators of
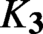 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 24 May 2021, e40
-
- Article
-
- You have access
- Open access
- Export citation
NONDIVISIBILITY AMONG IRREDUCIBLE CHARACTER CO-DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 68-74
- Print publication:
- February 2022
-
- Article
- Export citation
INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-116
- Print publication:
- February 2022
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
- Print publication:
- February 2022
-
- Article
- Export citation
1324- and 2143-avoiding Kazhdan–Lusztig immanants and k-positivity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 May 2021, pp. 52-82
- Print publication:
- February 2023
-
- Article
- Export citation
ON THE RANK OF A VERBAL SUBGROUP OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 145-159
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- Export citation