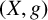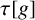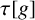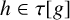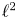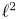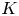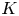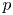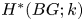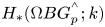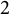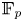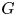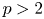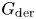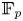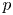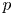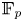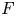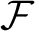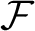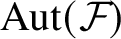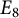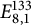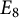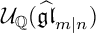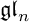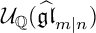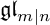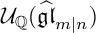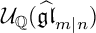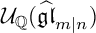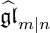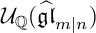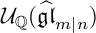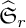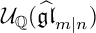Refine listing
Actions for selected content:
1959 results in 20xxx
ORIENTATION OF PIECEWISE POWERS OF A MINIMAL HOMEOMORPHISM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 15 November 2021, pp. 226-256
- Print publication:
- October 2022
-
- Article
- Export citation
Maximal subgroups of nontorsion Grigorchuk–Gupta–Sidki groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 825-844
- Print publication:
- December 2022
-
- Article
- Export citation
Steenrod operators, the Coulomb branch and the Frobenius twist
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2021, pp. 2494-2552
- Print publication:
- November 2021
-
- Article
- Export citation
Folding-like techniques for CAT(0) cube complexes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 28 October 2021, pp. 227-238
- Print publication:
- July 2022
-
- Article
- Export citation
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
The first $\ell ^{2}$
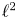 -betti number and groups acting on trees
-betti number and groups acting on trees
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. 916-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTS, CROSSED PRODUCTS AND INVERSE SEMIGROUP COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 253-288
- Print publication:
- April 2023
-
- Article
- Export citation
Wall-crossings and a categorification of K-theory stable bases of the Springer resolution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2341-2376
- Print publication:
- November 2021
-
- Article
- Export citation
MONOMIAL AND MONOLITHIC CHARACTERS OF FINITE SOLVABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 05 October 2021, pp. 440-448
- Print publication:
- June 2022
-
- Article
- Export citation
ISOLATED SUBGROUPS OF FINITE p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 449-457
- Print publication:
- June 2022
-
- Article
- Export citation
Semigroups whose right ideals are finitely generated
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 01 October 2021, pp. 848-883
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A bimodule description of the Hecke category
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 2133-2159
- Print publication:
- October 2021
-
- Article
- Export citation
On holomorphic reflexivity conditions for complex Lie groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 800-821
-
- Article
- Export citation
Massey products in the homology of the loop space of a p-completed classifying space: finite groups with cyclic Sylow p-subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 908-915
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation
Central elements in affine mod p Hecke algebras via perverse
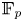 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2215-2241
- Print publication:
- October 2021
-
- Article
- Export citation
Extensions of homomorphisms between localities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 14 September 2021, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Allison–Faulkner construction of
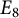 $E_8$
$E_8$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 686-701
- Print publication:
- September 2022
-
- Article
- Export citation
ON SEPARABILITY FINITENESS CONDITIONS IN SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 402-430
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A REALIZATION OF THE ENVELOPING SUPERALGEBRA
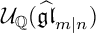 $ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
$ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 516-551
- Print publication:
- September 2022
-
- Article
- Export citation