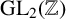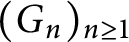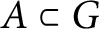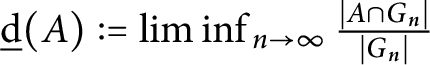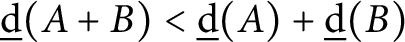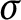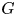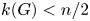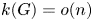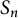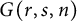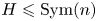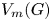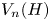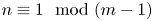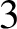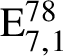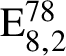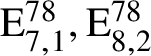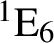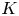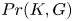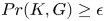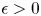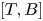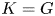Refine listing
Actions for selected content:
1959 results in 20xxx
AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 102-112
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
Kneser’s theorem in
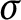 $\sigma $-finite abelian groups
$\sigma $-finite abelian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 936-942
- Print publication:
- December 2022
-
- Article
- Export citation
GROUPS WITH A GIVEN NUMBER OF NONPOWER SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 315-319
- Print publication:
- October 2022
-
- Article
- Export citation
Weak amenability of free products of hyperbolic and amenable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 698-701
- Print publication:
- September 2022
-
- Article
- Export citation
ON MAXIMAL SUBGROUPS OF IDEMPOTENT-GENERATED SEMIGROUPS ASSOCIATED WITH BIORDERED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 January 2022, pp. 341-343
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
Commutator length of powers in free products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 102-119
-
- Article
- Export citation
INTERPRETING A FIELD IN ITS HEISENBERG GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 December 2021, pp. 1215-1230
- Print publication:
- September 2022
-
- Article
- Export citation
On the number of conjugacy classes of a primitive permutation group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 115-136
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariants for metabelian groups of prime power exponent, colorings, and stairs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 December 2021, pp. 267-297
- Print publication:
- February 2023
-
- Article
- Export citation
PRINCIPAL RADICAL SYSTEMS, LEFSCHETZ PROPERTIES, AND PERFECTION OF SPECHT IDEALS OF TWO-ROWED PARTITIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 690-730
- Print publication:
- September 2022
-
- Article
- Export citation
On the multiplication of spherical functions of reductive spherical pairs of type A
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 341-374
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomiality of factorizations in reflection groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 245-266
- Print publication:
- February 2023
-
- Article
- Export citation
Some embeddings between symmetric R. thompson groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 1-18
-
- Article
- Export citation
Abelian actions on compact nonorientable Riemann surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 634-648
- Print publication:
- September 2022
-
- Article
- Export citation
On the construction of tame supercuspidal representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 03 January 2022, pp. 2733-2746
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum to ‘Endoscopy for Hecke categories, character sheaves and representations’
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 30 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Frucht property in the quantum group setting
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 November 2021, pp. 603-633
- Print publication:
- September 2022
-
- Article
- Export citation
On the Tits–Weiss conjecture and the Kneser–Tits conjecture for
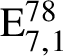 $\mathrm {E}^{78}_{7,1}$ and
$\mathrm {E}^{78}_{7,1}$ and 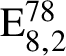 $\mathrm {E}^{78}_{8,2}$ (With an Appendix by R. M. Weiss)
$\mathrm {E}^{78}_{8,2}$ (With an Appendix by R. M. Weiss)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 23 November 2021, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the commuting probability for subgroups of a finite group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 1551-1564
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation