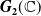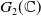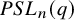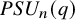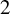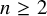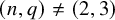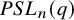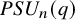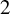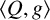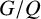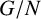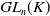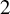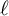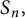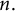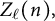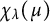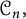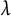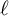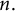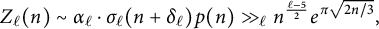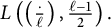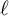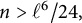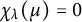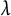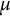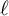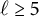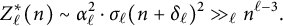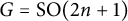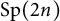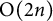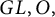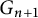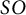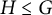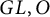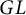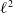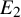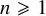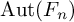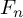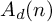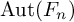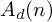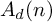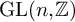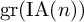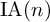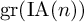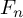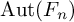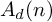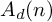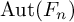Refine listing
Actions for selected content:
1959 results in 20xxx
ON 2-TRANSITIVE SETS OF EQUIANGULAR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 134-145
- Print publication:
- February 2023
-
- Article
- Export citation
COHOMOLOGICAL MACKEY 2-FUNCTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 August 2022, pp. 279-309
- Print publication:
- January 2024
-
- Article
- Export citation
On the dynamics of extensions of free-abelian times free groups endomorphisms to the completion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 12 August 2022, pp. 705-735
-
- Article
- Export citation
Polyhedral groups in
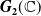 $\textbf{G}_{\textbf{2}}(\mathbb C)$
$\textbf{G}_{\textbf{2}}(\mathbb C)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. S123-S128
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of the groups
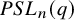 $PSL_n(q)$ and
$PSL_n(q)$ and 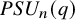 $PSU_n(q)$ by their
$PSU_n(q)$ by their 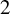 $2$-fusion systems, q odd
$2$-fusion systems, q odd
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 05 August 2022, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal order Abelian subgroups of Coxeter groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 02 August 2022, pp. 114-120
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH A LARGE PERMUTABLY EMBEDDED SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 276-283
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME PRODUCTS OF SUBGROUPS AND VANISHING CONJUGACY CLASS SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 271-275
- Print publication:
- April 2023
-
- Article
- Export citation
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
- Print publication:
- January 2023
-
- Article
- Export citation
On homomorphisms into Weyl modules corresponding to partitions with two parts
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 272-283
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximum likelihood estimation for tensor normal models via castling transforms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 01 July 2022, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF GALOIS ACTIONS OF TORSION ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 2943-2985
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-isolated blocks and the Alperin–McKay conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 June 2022, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros in the character tables of symmetric groups with an
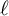 $\ell $-core index
$\ell $-core index
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 June 2022, pp. 467-476
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1343-1368
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicity one theorems over positive characteristic
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 June 2022, pp. 1018-1044
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Groups whose Chermak–Delgado lattice is a subgroup lattice of an abelian group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 443-449
- Print publication:
- June 2023
-
- Article
- Export citation
A note on the rational homological dimension of lattices in positive characteristic
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 138-140
- Print publication:
- January 2023
-
- Article
- Export citation
Parametrised moduli spaces of surfaces as infinite loop spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACTIONS OF AUTOMORPHISM GROUPS OF FREE GROUPS ON SPACES OF JACOBI DIAGRAMS. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1-69
- Print publication:
- January 2024
-
- Article
- Export citation