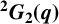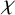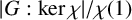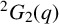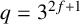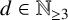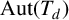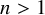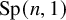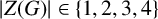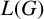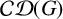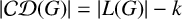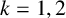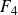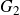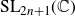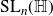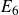Refine listing
Actions for selected content:
1959 results in 20xxx
A correspondence between inverse subsemigroups, open wide subgroupoids and cartan intermediate C*-subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 October 2022, pp. 861-879
-
- Article
- Export citation
Central limit theorems for counting measures in coarse negative curvature
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 03 November 2022, pp. 1980-2013
- Print publication:
- October 2022
-
- Article
- Export citation
RECOGNISING REE GROUPS
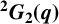 $\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET
$\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 28 September 2022, pp. 125-132
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE STABLE LIMIT DAHA AND THE DOUBLE DYCK PATH ALGEBRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 26 September 2022, pp. 379-424
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS IN WHICH ALL LARGE SUBGROUPS HAVE BOUNDED NEAR DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 456-463
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTER STACKS ARE PORC COUNT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 289-310
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Products of derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME CRITERIA FOR SOLVABILITY AND NILPOTENCY OF FINITE GROUPS BY STRONGLY MONOLITHIC CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 120-124
- Print publication:
- August 2023
-
- Article
- Export citation
GROUPS ACTING ON TREES WITH PRESCRIBED LOCAL ACTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 240-288
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic subgroups of large-type Artin groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 393-414
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small non-Leighton two-complexes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 385-391
- Print publication:
- March 2023
-
- Article
- Export citation
Stability conditions for contraction algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kernels of localities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for surface groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 1850-1877
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The equivalence between rational G-sheaves and rational G-Mackey functors for profinite G
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 345-368
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SYLOW CLASSES OF REFLECTION SUBGROUPS AND PSEUDO-LEVI SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 508-510
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Quaternionic hyperbolic lattices of minimal covolume
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 25 August 2022, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH ABNORMAL MINIMAL NONNILPOTENT SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 261-270
- Print publication:
- April 2023
-
- Article
- Export citation
FINITE GROUPS WITH LARGE CHERMAK–DELGADO LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 451-455
- Print publication:
- June 2023
-
- Article
- Export citation
On the profinite rigidity of lattices in higher rank Lie groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 369-384
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation