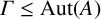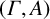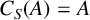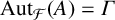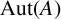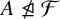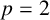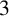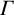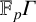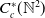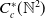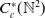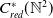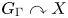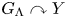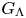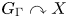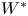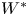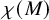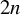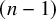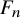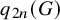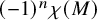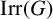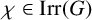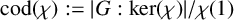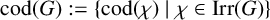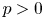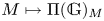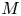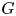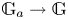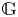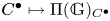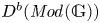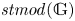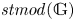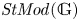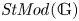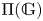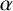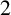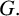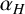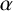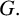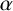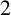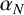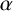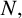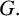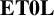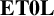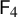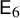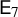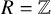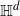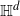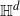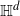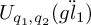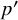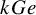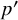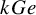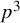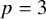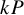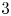Refine listing
Actions for selected content:
1959 results in 20xxx
NONREALIZABILITY OF CERTAIN REPRESENTATIONS IN FUSION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 257-288
- Print publication:
- April 2024
-
- Article
- Export citation
Phase transitions for non-singular Bernoulli actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 353-382
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL CATEGORIES AND PRO-p IWAHORI–HECKE MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1029-1076
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KMS states on
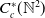 $C_c^{*}(\mathbb{N}^2)$
$C_c^{*}(\mathbb{N}^2)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 501-528
- Print publication:
- September 2023
-
- Article
- Export citation
Orbit equivalence rigidity of irreducible actions of right-angled Artin groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 860-887
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal Euler characteristics for even-dimensional manifolds with finite fundamental group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some products of finite groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 89-99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CHARACTERISATION OF SPORADIC SIMPLE GROUPS BY CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 57-66
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Support varieties and stable categories for algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 27 March 2023, pp. 746-779
- Print publication:
- April 2023
-
- Article
- Export citation
HALL SUBGROUPS AND
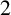 $2$-COCYCLE REGULARITY
$2$-COCYCLE REGULARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 24 March 2023, pp. 51-56
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRICT REGULARITY FOR
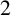 $2$-COCYCLES OF FINITE GROUPS
$2$-COCYCLES OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 24 March 2023, pp. 45-50
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite image homomorphisms of the braid group and its generalizations
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 March 2023, pp. 430-445
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
MULTIPLICATION TABLES AND WORD-HYPERBOLICITY IN FREE PRODUCTS OF SEMIGROUPS, MONOIDS AND GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 396-430
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Braiding groups of automorphisms and almost-automorphisms of trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 555-593
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Albert algebras over
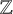 $\mathbb {Z}$ and other rings
$\mathbb {Z}$ and other rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 March 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thin-ended clusters in percolation in
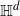 $\mathbb{H}^d$
$\mathbb{H}^d$
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 581-610
- Print publication:
- June 2023
-
- Article
- Export citation
A CATEGORICAL QUANTUM TOROIDAL ACTION ON THE HILBERT SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 March 2023, pp. 897-940
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of blocks with normal defect and abelian
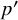 $p'$ inertial quotient
$p'$ inertial quotient
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 March 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isolations of geodesic planes in the frame bundle of a hyperbolic 3-manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 488-529
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation