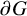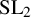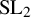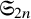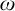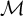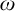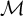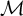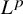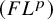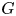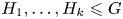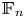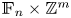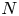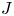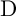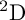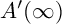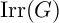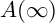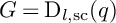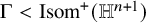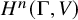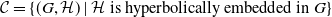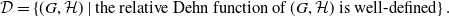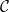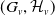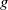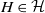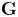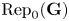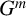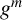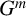Refine listing
Actions for selected content:
1959 results in 20xxx
Stability for hyperbolic groups acting on boundary spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A combinatorial model for the transition matrix between the Specht and
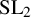 $\operatorname {SL}_2$-web bases
$\operatorname {SL}_2$-web bases
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 September 2023, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASSIFICATION OF
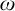 $\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
$\omega $-CATEGORICAL MONADICALLY STABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 460-495
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CAYLEY GRAPHS AND GRAPHICAL REGULAR REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 161-162
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Żuk’s criterion for Banach spaces and random groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 September 2023, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersection configurations in free and free times free-abelian groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1552-1582
- Print publication:
- October 2024
-
- Article
- Export citation
Fixed point conditions for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 345-351
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
- Export citation
EXTENSIONS OF CHARACTERS IN TYPE D AND THE INDUCTIVE MCKAY CONDITION, I
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 08 September 2023, pp. 906-958
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Reidemeister spectrum of finite abelian groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 940-959
-
- Article
- Export citation
Quantum symmetries of Cayley graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 655-686
- Print publication:
- September 2023
-
- Article
- Export citation
Cusps, Kleinian groups, and Eisenstein series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 August 2023, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative Dehn functions, hyperbolically embedded subgroups and combination theorems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 25 August 2023, pp. 1-23
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hecke category actions via Smith–Treumann theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 23 August 2023, pp. 2089-2124
- Print publication:
- October 2023
-
- Article
- Export citation
Proper Ehresmann semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 758-788
-
- Article
- Export citation
Corrigendum: Von Neumann algebras and extensions of inverse semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 919-922
-
- Article
-
- You have access
- HTML
- Export citation
Tame or wild Toeplitz shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1379-1417
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Connected components of affine Deligne–Lusztig varieties for unramified groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 17 August 2023, pp. 2051-2088
- Print publication:
- October 2023
-
- Article
- Export citation
On the structure of lower bounded HNN extensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 August 2023, pp. 697-715
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH FEW NONPOWER SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 10 August 2023, pp. 529-540
- Print publication:
- June 2024
-
- Article
- Export citation