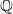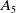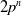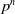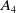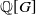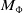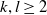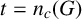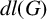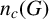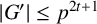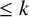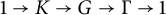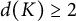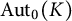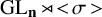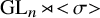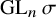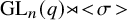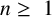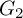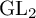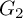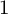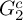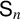Refine listing
Actions for selected content:
1959 results in 20xxx
Leopoldt-type theorems for non-abelian extensions of
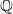 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dehn functions of mapping tori of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 252-289
- Print publication:
- May 2024
-
- Article
- Export citation
Classifying spaces for families of abelian subgroups of braid groups, RAAGs and graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 290-307
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 2700-2736
- Print publication:
- September 2024
-
- Article
- Export citation
Hypercontractivity on the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Base sizes of primitive groups of diagonal type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 04 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a variant of the product replacement algorithm
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 January 2024, pp. 221-228
- Print publication:
- January 2024
-
- Article
- Export citation
SOLVABLE GROUPS WHOSE NONNORMAL SUBGROUPS HAVE FEW ORDERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 121-128
- Print publication:
- August 2024
-
- Article
- Export citation
THE PRO-
 $\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
$\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 363-383
- Print publication:
- June 2024
-
- Article
- Export citation
Higher dimensional algebraic fiberings for pro-p groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 300-323
- Print publication:
- February 2025
-
- Article
- Export citation
The spherical growth series of Dyer groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 168-187
-
- Article
- Export citation
E-Polynomials of Generic
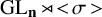 $\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
$\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL SUBMONOIDS AND CONGRUENCES ON A MONOID
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 331-362
- Print publication:
- June 2024
-
- Article
- Export citation
Levy and Thurston obstructions of finite subdivision rules
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 2649-2699
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING DISCRETE, LEVEL-
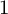 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 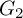 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 2127-2157
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITELY PRESENTED INVERSE SEMIGROUPS WITH FINITELY MANY IDEMPOTENTS IN EACH
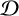 $\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
$\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 384-398
- Print publication:
- June 2024
-
- Article
- Export citation
A BOREL MAXIMAL COFINITARY GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 11 December 2023, pp. 808-821
- Print publication:
- June 2025
-
- Article
- Export citation
COMMON ZEROS OF IRREDUCIBLE CHARACTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 105-129
- Print publication:
- October 2024
-
- Article
- Export citation
A question of Frohardt on
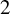 $2$-groups, skew translation quadrangles of even order and cyclic STGQs
$2$-groups, skew translation quadrangles of even order and cyclic STGQs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON RESIDUES AND CONJUGACIES FOR GERMS OF 1-D PARABOLIC DIFFEOMORPHISMS IN FINITE REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1821-1855
- Print publication:
- July 2024
-
- Article
- Export citation