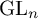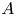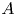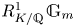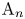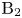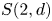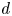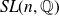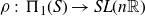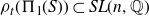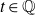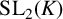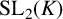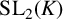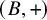Refine listing
Actions for selected content:
1959 results in 20xxx
Orthogonality relations for deep level Deligne–Lusztig schemes of Coxeter type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 May 2024, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SET OF BETTI ELEMENTS OF A PUISEUX MONOID
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 20 May 2024, pp. 80-92
- Print publication:
- February 2025
-
- Article
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
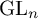 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 May 2024, pp. 41-116
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 830-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit pretrees for free group automorphisms: existence
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak approximation on the norm one torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1304-1348
- Print publication:
- June 2024
-
- Article
- Export citation
Hyperbolic one-relator groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Donkin's tilting module conjecture II: counterexamples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1167-1193
- Print publication:
- June 2024
-
- Article
- Export citation
CORRECTION TO ‘AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 30 April 2024, pp. 171-176
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
- Print publication:
- January 2025
-
- Article
- Export citation
Maximal subgroups of a family of iterated monodromy groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 541-562
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zariski dense surface subgroups in
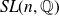 $SL(n,\mathbb{Q})$ with odd
$SL(n,\mathbb{Q})$ with odd  $n$
$n$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 643-653
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal monoids generating varieties with complex subvariety lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 617-642
-
- Article
- Export citation
BASIC NONARCHIMEDEAN JØRGENSEN THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 273-287
- Print publication:
- December 2024
-
- Article
- Export citation
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CHARACTERISATION OF SOLUBLE
 ${PST}$-GROUPS
${PST}$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 520-527
- Print publication:
- December 2024
-
- Article
- Export citation
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 440-448
- Print publication:
- May 2024
-
- Article
- Export citation
Hyperfiniteness of boundary actions of acylindrically hyperbolic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation