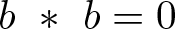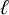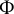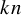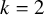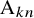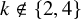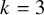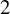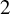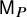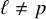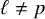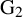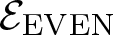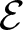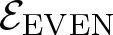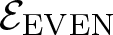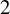Refine listing
Actions for selected content:
1959 results in 20xxx
A note on right-nil and strong-nil skew braces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-9
-
- Article
- Export citation
A local-global principle for unipotent characters
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 December 2024, e125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NUMERICAL SEMIGROUPS FROM RATIONAL MATRICES II: MATRICIAL DIMENSION DOES NOT EXCEED MULTIPLICITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 155-162
- Print publication:
- August 2025
-
- Article
- Export citation
Uniform bounded elementary generation of Chevalley groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 December 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit trees for free group automorphisms: universality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e122
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A complete classification of shuffle groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 04 December 2024, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On split quasi-hereditary covers and Ringel duality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON NEIGHBOURHOODS IN THE ENHANCED POWER GRAPH ASSOCIATED WITH A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 149-154
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting homomorphisms from surface groups to finite groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 29 November 2024, pp. 141-153
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On finite presentability of subsemigroups of the monogenic free inverse semigroup
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 November 2024, pp. 185-196
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regular Schur labeled skew shape posets and their 0-Hecke modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum wreath products and Schur–Weyl duality I
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lifting G-Valued Galois Representations when
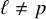 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The planar 3-colorable subgroup ε of Thompson’s group F and its even part
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 173-197
-
- Article
- Export citation
The line bundles on the moduli stack of principal bundles on families of curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 80-127
-
- Article
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1403-1443
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tilings of the hyperbolic space and Lipschitz functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1985-2005
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
All Kronecker coefficients are reduced Kronecker coefficients
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fusion Systems and Rank
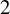 $2$ Simple Groups of Lie Type
$2$ Simple Groups of Lie Type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 November 2024, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation