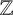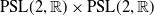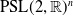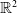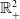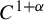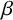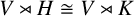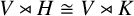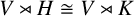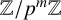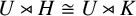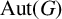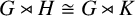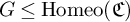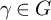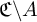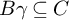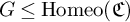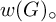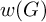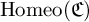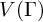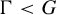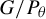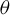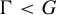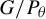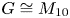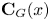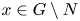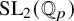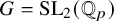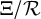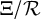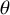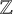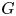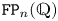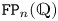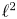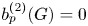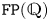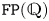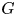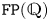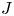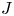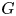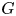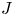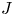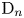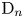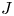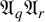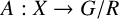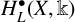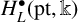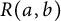Refine listing
Actions for selected content:
1959 results in 20xxx
A CHARACTERISATION OF SEMIGROUPS WITH ONLY COUNTABLY MANY SUBDIRECT PRODUCTS WITH
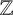 $\mathbb {Z}$
$\mathbb {Z}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 314-323
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic actions of higher rank lattices come from rank-one factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 961-988
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weyl chamber length compactification of the
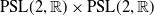 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 11-33
- Print publication:
- January 2025
-
- Article
- Export citation
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1177-1198
- Print publication:
- April 2025
-
- Article
- Export citation
ISOMORPHISM OF RELATIVE HOLOMORPHS AND MATRIX SIMILARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 September 2024, pp. 298-313
- Print publication:
- April 2025
-
- Article
- Export citation
SUFFICIENT CONDITIONS FOR A GROUP OF HOMEOMORPHISMS OF THE CANTOR SET TO BE TWO-GENERATED
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 2825-2858
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-concentration property of Patterson–Sullivan measures for Anosov subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 884-893
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The structure of finite groups whose elements outside a normal subgroup have prime power orders
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-20
-
- Article
- Export citation
KRONECKER COEFFICIENTS FOR (DUAL) SYMMETRIC INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 65-90
- Print publication:
- February 2025
-
- Article
- Export citation
CONGRUENCE SUBGROUPS OF BRAID GROUPS AND CRYSTALLOGRAPHIC QUOTIENTS. PART I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 145-163
- Print publication:
- April 2025
-
- Article
- Export citation
Stability in the category of smooth mod-p representations of
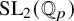 ${\mathrm {SL}}_2(\mathbb {Q}_p)$
${\mathrm {SL}}_2(\mathbb {Q}_p)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds on multiplicities of symmetric pairs of finite groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Centralisers of linear growth automorphisms of free groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 219-240
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved algebraic fibrings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2203-2227
- Print publication:
- September 2024
-
- Article
- Export citation
The
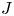 $J$-invariant over splitting fields of Tits algebras
$J$-invariant over splitting fields of Tits algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 2100-2114
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENUMERATION OF GROUPS IN SOME SPECIAL VARIETIES OF A-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 27 August 2024, pp. 107-117
- Print publication:
- February 2025
-
- Article
- Export citation
Finitely generated simple sharply 2-transitive groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1941-1957
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTING CENTRALISERS IN [FINITELY GENERATED FREE]-BY-CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 June 2024, pp. 118-127
- Print publication:
- February 2025
-
- Article
- Export citation
TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 187-238
- Print publication:
- October 2024
-
- Article
- Export citation
Strong digraph groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 991-1000
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation