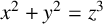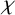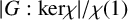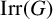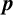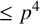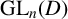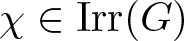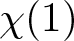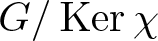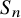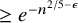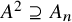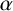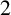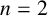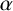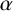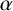Refine listing
Actions for selected content:
1959 results in 20xxx
Centers of Artin groups defined on cones
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 44-50
-
- Article
- Export citation
Prosoluble subgroups of free profinite products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 November 2024, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF
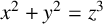 $x^2+y^2=z^3$
$x^2+y^2=z^3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 57-66
- Print publication:
- August 2025
-
- Article
- Export citation
THE PRODUCT OF A GENERALIZED QUATERNION GROUP AND A CYCLIC GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 31-64
- Print publication:
- February 2025
-
- Article
- Export citation
ON THE CODEGREES OF STRONGLY MONOLITHIC CHARACTERS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 283-289
- Print publication:
- April 2025
-
- Article
- Export citation
RATIONAL REPRESENTATIONS AND RATIONAL GROUP ALGEBRA OF VZ
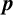 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-30
- Print publication:
- February 2025
-
- Article
- Export citation
LOCALLY NILPOTENT SUBGROUPS OF
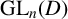 $\mathrm {GL}_n(D)$
$\mathrm {GL}_n(D)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 128-138
- Print publication:
- August 2025
-
- Article
- Export citation
Kernels of minimal characters of solvable groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1167-1170
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An update on Haiman’s conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved covering results for conjugacy classes of symmetric groups via hypercontractivity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic orders and graphs of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 1125-1136
-
- Article
- Export citation
VERTEX-PRIMITIVE s-ARC-TRANSITIVE DIGRAPHS OF ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 16 October 2024, pp. 566-567
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON MINIMAL DEGREES OF QUOTIENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 177-179
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
FINITE GROUPS WHOSE CHARACTER CODEGREES ARE CONSECUTIVE INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 513-517
- Print publication:
- June 2025
-
- Article
- Export citation
Effective dynamical systems beyond dimension zero and factors of SFTs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1329-1369
- Print publication:
- May 2025
-
- Article
- Export citation
A NOTE ON THE FINITELY GENERATED FIXED SUBGROUP PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 530-540
- Print publication:
- June 2025
-
- Article
- Export citation
Gassmann triples with special cycle types and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1115-1124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS–SCHUR INDICATORS FOR PROJECTIVE CHARACTERS WITH APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 290-297
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON NONINNER AUTOMORPHISMS OF SOME FINITE P-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 524-529
- Print publication:
- June 2025
-
- Article
- Export citation