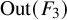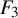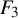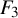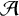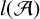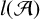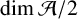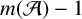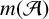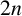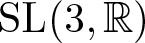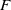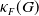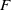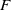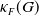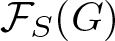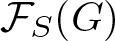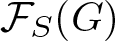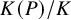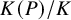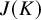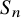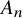Refine listing
Actions for selected content:
1959 results in 20xxx
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF PAIRWISE NONCOMMUTING SETS IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 497-504
- Print publication:
- December 2025
-
- Article
- Export citation
An Iwahori theoretic mod
 $p$ local Langlands correspondence
$p$ local Langlands correspondence
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 805-817
- Print publication:
- September 2025
-
- Article
- Export citation
The conjugacy problem for
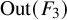 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELEMENTARY PROOFS OF THE DIAMETER BOUNDS FOR POWER GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 505-508
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COHOMOLOGY OF p-ADIC DELIGNE-LUSZTIG SCHEMES OF COXETER TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1429-1462
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN UPPER BOUND ON THE LENGTH OF AN ALGEBRA AND ITS APPLICATION TO THE GROUP ALGEBRA OF THE DIHEDRAL GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 139-148
- Print publication:
- August 2025
-
- Article
- Export citation
Hyperbolic Metric Spaces and Stochastic Embeddings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometrization of the Satake transform for mod p Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Right-angled Artin groups and the cohomology basis graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 634-654
-
- Article
- Export citation
Constructing skew left braces whose additive group has trivial centre
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 797-804
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly dense representations of surface groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 583-593
-
- Article
- Export citation
Abelian supplements in almost simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bender–Knuth Billiards in Coxeter Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal linear sofic approximations of countable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 245-268
- Print publication:
- May 2025
-
- Article
- Export citation
Conditions for the supersolvability of
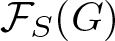 $\mathcal{F}_{S}(G)$
$\mathcal{F}_{S}(G)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 23 January 2025, pp. 566-572
-
- Article
- Export citation
A single source theorem for primitive points on curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Closed approximate subgroups: compactness, amenability and approximate lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ekedahl–Oort stratification and the semi-module stratification
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Membership problems for positive one-relator groups and one-relation monoids
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation