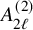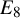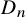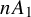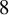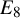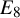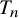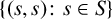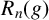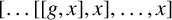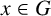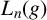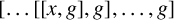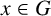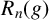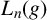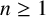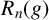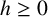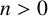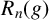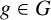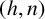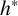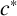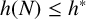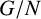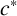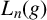Refine listing
Actions for selected content:
1959 results in 20xxx
On the structures of the Johnson cokernels of the basis-conjugating automorphism groups of free groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-29
-
- Article
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundaries and equivariant maps for ergodic groupoids
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-32
-
- Article
- Export citation
Derived equivalences for trigonometric double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orthogonal roots, Macdonald representations, and quasiparabolic sets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thompson’s group T has quadratic Dehn function
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMIGROUP CONGRUENCES AND SUBSEMIGROUPS OF THE DIRECT SQUARE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH DENSE TRANSITIVELY NORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-7
-
- Article
- Export citation
ON THE LARGEST CHARACTER DEGREE OF SOLVABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Morava J-invariant
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 July 2025, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for graphs of free groups with cyclic edge groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1576-1614
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random walks and contracting elements I: deviation inequality and limit laws
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1512-1575
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGHT ENGEL CONDITIONS FOR ORDERABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 June 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTER VARIETIES, EARTHQUAKES AND ESSENTIAL SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 27 June 2025, pp. 387-388
- Print publication:
- October 2025
-
- Article
-
- You have access
- HTML
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Splines on Cayley graphs of the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 June 2025, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steiner Coset Partitions of Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1359-1373
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rotation groups virtually embed into right-angled rotation groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-25
-
- Article
- Export citation
Character and class parameters from entries of character tables of symmetric groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 05 June 2025, pp. 439-447
- Print publication:
- September 2025
-
- Article
- Export citation