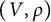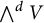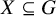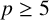Refine listing
Actions for selected content:
1959 results in 20xxx
Rigidity of mapping class groups MOD powers of twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-71
-
- Article
- Export citation
3-manifold spine cyclic presentations with seldom seen Whitehead graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A hyperbolic free-by-cyclic group determined by its finite quotients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 500-502
- Print publication:
- September 2025
-
- Article
- Export citation
The Klein bottle has stably unbounded homeomorphism group
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 494-499
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 869-897
-
- Article
- Export citation
On the Fourier coefficients of word maps on unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 681-713
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On exterior powers of reflection representations, II
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-23
-
- Article
- Export citation
A Shelah group in ZFC
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linearity of compact R-analytic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 787-794
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON IDENTITIES OF REES QUOTIENTS OF FREE INVERSE SEMIGROUPS DEFINED BY POSITIVE RELATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 335-367
- Print publication:
- June 2025
-
- Article
- Export citation
A Pride–Guba–Sapir exact sequence for the relation bimodule of an associative algebra
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 467-474
- Print publication:
- September 2025
-
- Article
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 3090-3147
- Print publication:
- October 2025
-
- Article
- Export citation
Generalised Temperley–Lieb algebras of type G(r, p, n)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 193-227
- Print publication:
- March 2025
-
- Article
- Export citation
Stratified braid groups: monodromy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 259-292
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform models and short curves for random 3-manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 27 June 2025, pp. 447-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Are free groups of different ranks bi-invariantly quasi-isometric?
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 356-364
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXCEPTIONAL GROUPS OF ORDER
 $p^6$ FOR PRIMES
$p^6$ FOR PRIMES 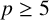 $p\geq 5$
$p\geq 5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 485-496
- Print publication:
- December 2025
-
- Article
- Export citation
Reversibility and transitivity of semigroup actions on homogeneous spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-20
-
- Article
- Export citation