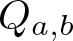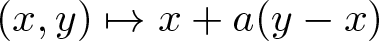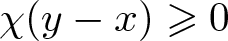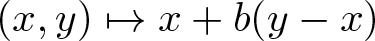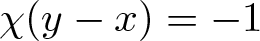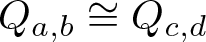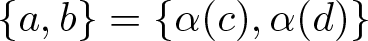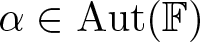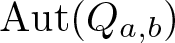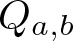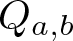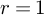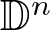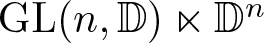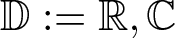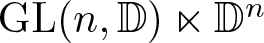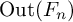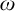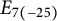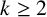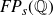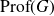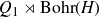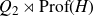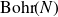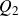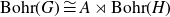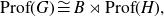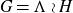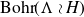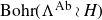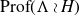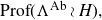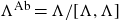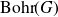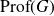Refine listing
Actions for selected content:
1959 results in 20xxx
Isomorphisms of quadratic quasigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 24 November 2023, pp. 1085-1109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GROUPS OF UNITS OF SPECIAL AND ONE-RELATOR INVERSE MONOIDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 November 2023, pp. 1875-1918
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODEL-THEORETIC CONNECTED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 50-79
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reversibility of affine transformations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 08 November 2023, pp. 1217-1228
-
- Article
- Export citation
ON ENDOMORPHISMS OF EXTENSIONS IN TANNAKIAN CATEGORIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 07 November 2023, pp. 103-114
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ZARISKI TOPOLOGY ON ENDOMORPHISM MONOIDS OF OMEGA-CATEGORICAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prefix monoids of groups and right units of special inverse monoids
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 30 October 2023, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FAITHFULNESS OF THE 2-BRAID GROUP VIA ZIGZAG ALGEBRA IN TYPE B
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 67-84
- Print publication:
- August 2024
-
- Article
- Export citation
Distortion element in the automorphism group of a full shift
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1757-1817
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded cohomology is not a profinite invariant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TORIC REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 171-199
- Print publication:
- April 2024
-
- Article
- Export citation
On subdirect products of type FPn of limit groups over Droms RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 417-440
- Print publication:
- March 2024
-
- Article
- Export citation
FINITE BASIS PROBLEM FOR INVOLUTION MONOIDS OF ORDER FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 350-364
- Print publication:
- April 2024
-
- Article
- Export citation
On Bohr compactifications and profinite completions of group extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 373-393
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EXTERIOR POWERS OF REFLECTION REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 90-102
- Print publication:
- August 2024
-
- Article
- Export citation
TRIPLE-PRODUCT-FREE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 129-135
- Print publication:
- August 2024
-
- Article
- Export citation
A new upper bound for the asymptotic dimension of RACGs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 338-349
- Print publication:
- June 2024
-
- Article
- Export citation
Some torsion-free solvable groups with few subquotients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 279-286
- Print publication:
- March 2024
-
- Article
- Export citation
A lattice theoretical interpretation of generalized deep holes of the Leech lattice vertex operator algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation