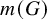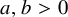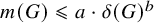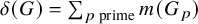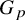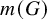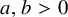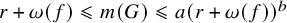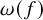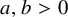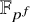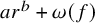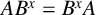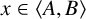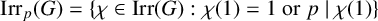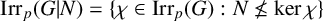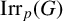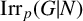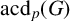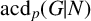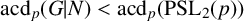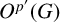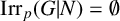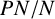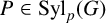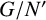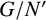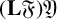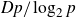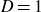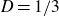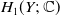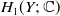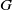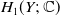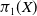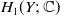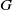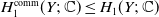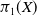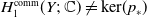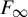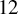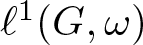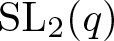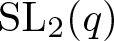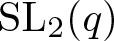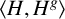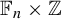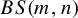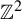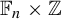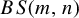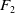Refine listing
Actions for selected content:
1959 results in 20xxx
The maximal size of a minimal generating set
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 August 2023, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH HEREDITARILY G-PERMUTABLE SCHMIDT SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 28 July 2023, pp. 522-528
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE SOLVABLE TIDY GROUPS ARE DETERMINED BY HALL SUBGROUPS WITH TWO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 342-349
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON p-SOLVABILITY AND AVERAGE CHARACTER DEGREE IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 507-511
- Print publication:
- June 2024
-
- Article
- Export citation
A presentation for the Eisenstein-Picard modular group in three complex dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 625-654
- Print publication:
- September 2023
-
- Article
- Export citation
HALL CLASSES OF GROUPS WITH A LOCALLY FINITE OBSTRUCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 16-43
- Print publication:
- August 2024
-
- Article
- Export citation
Continuum of allosteric actions for non-amenable surface groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1581-1596
- Print publication:
- June 2024
-
- Article
- Export citation
SELF-DIVISIBLE ULTRAFILTERS AND CONGRUENCES IN
 $\beta {\mathbb {Z}}$
$\beta {\mathbb {Z}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1180-1197
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime divisors and the number of conjugacy classes of finite groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subrepresentations in the homology of finite covers of graphs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. 582-594
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finitely presented left orderable monsters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 July 2023, pp. 1367-1378
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weights in a Benson-Solomon block
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Dales–Żelazko conjecture for Beurling algebras on discrete groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 613-624
-
- Article
- Export citation
Trivial source character tables of
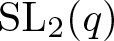 $\operatorname{SL}_2(q)$, part II
$\operatorname{SL}_2(q)$, part II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 689-709
-
- Article
- Export citation
LOCALLY FINITE SIMPLE GROUPS WHOSE NONNILPOTENT SUBGROUPS ARE PRONORMAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 512-521
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Groups of small period growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 27 June 2023, pp. 625-641
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the algebra of elliptic curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 548-556
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONDITIONAL FLATNESS, FIBERWISE LOCALIZATIONS, AND ADMISSIBLE REFLECTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 200-220
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly aperiodic SFTs on generalized Baumslag–Solitar groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1209-1238
- Print publication:
- May 2024
-
- Article
- Export citation
Continuously many quasi-isometry classes of residually finite groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 569-572
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation