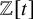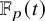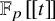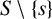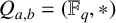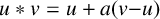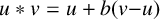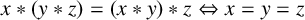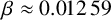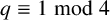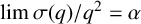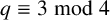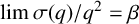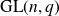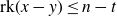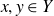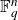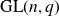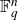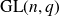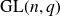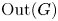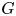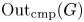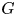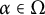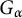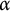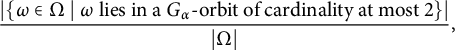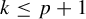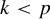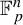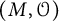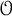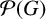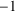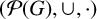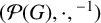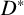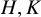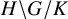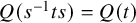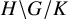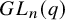Refine listing
Actions for selected content:
1959 results in 20xxx
Grassmanniennes affines tordues sur les entiers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH INDEPENDENT GENERATING SETS OF ONLY TWO SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 449-458
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF QUADRATIC ORTHOMORPHISMS THAT PRODUCE MAXIMALLY NONASSOCIATIVE QUASIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 20 February 2023, pp. 311-336
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersection theorems for finite general linear groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 129-160
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutation-finite quivers with real weights
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 February 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsymmetric exchanged braids and the Burau matrix
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 154-187
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHEN IS A NUMERICAL SEMIGROUP A QUOTIENT?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 67-76
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON LARGE ORBITS OF FINITE SOLVABLE GROUPS ON CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 438-442
- Print publication:
- December 2023
-
- Article
- Export citation
On automorphisms and splittings of special groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 232-305
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRUCTING MAXIMAL COFINITARY GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 30 January 2023, pp. 622-651
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite transitive groups having many suborbits of cardinality at most 2 and an application to the enumeration of Cayley graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 30 January 2023, pp. 345-366
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On higher-order Fourier analysis in characteristic p
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 27 January 2023, pp. 3971-4040
- Print publication:
- December 2023
-
- Article
- Export citation
A parametrization of sheets of conjugacy classes in bad characteristic
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 January 2023, pp. 976-983
- Print publication:
- September 2023
-
- Article
- Export citation
Conjugacy growth in the higher Heisenberg groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. S148-S169
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Bockstein maps and Massey products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 January 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMIRING AND INVOLUTION IDENTITIES OF POWER GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 354-374
- Print publication:
- December 2023
-
- Article
- Export citation
A NOTE ON SUBNORMAL SUBGROUPS IN DIVISION RINGS CONTAINING SOLVABLE SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 422-427
- Print publication:
- December 2023
-
- Article
- Export citation
On parabolic subgroups of symplectic reflection groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 401-413
- Print publication:
- May 2023
-
- Article
- Export citation
Hyperbolically embedded subgroups and quasi-isometries of pairs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 827-843
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double coset Markov chains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation