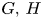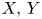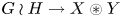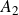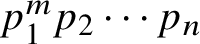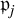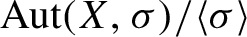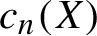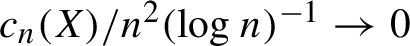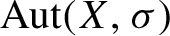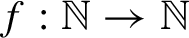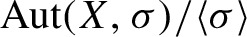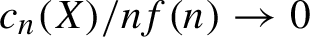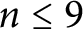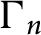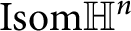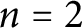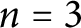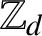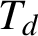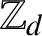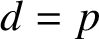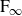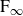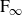Refine listing
Actions for selected content:
1959 results in 20xxx
Lamplighter groups, median spaces and Hilbertian geometry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 500-529
-
- Article
- Export citation
THE AUTOMORPHISM GROUP OF THE FRAÏSSÉ LIMIT OF FINITE HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 1310-1320
- Print publication:
- September 2023
-
- Article
- Export citation
Bouquets of curves in surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 90-97
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric actions and finite approximations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2464-2470
- Print publication:
- July 2023
-
- Article
- Export citation
EXTENSION BETWEEN SIMPLE MODULES OF PRO-p-IWAHORI HECKE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 2775-2804
- Print publication:
- November 2023
-
- Article
- Export citation
Groups generated by two twists along spherical sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 137-161
- Print publication:
- January 2023
-
- Article
- Export citation
ON THE CAYLEYNESS OF PRAEGER–XU GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 353-356
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hecke action on the principal block
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 19 July 2022, pp. 953-1019
- Print publication:
- May 2022
-
- Article
- Export citation
Left regular representations of Garside categories I. C*-algebras and groupoids
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. S53-S86
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLEX STRUCTURES ON STRATIFIED LIE ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 320-332
- Print publication:
- October 2022
-
- Article
- Export citation
Local finiteness and automorphism groups of low complexity subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1980-2001
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CAYLEY–ABELS GRAPHS AND INVARIANTS OF TOTALLY DISCONNECTED, LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 145-177
- Print publication:
- April 2023
-
- Article
- Export citation
REPRESENTING STRUCTURED SEMIGROUPS ON ÉTALE GROUPOID BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1-49
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A QUESTION OF MORETÓ
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 306-309
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special cube complexes revisited: a quasi-median generalization
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 April 2022, pp. 743-777
- Print publication:
- June 2023
-
- Article
- Export citation
Hyperbolic Coxeter groups of minimal growth rates in higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 06 April 2022, pp. 232-242
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLENOIDAL MAPS, AUTOMATIC SEQUENCES, VAN DER PUT SERIES, AND MEALY AUTOMATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 06 April 2022, pp. 78-109
- Print publication:
- February 2023
-
- Article
- Export citation
Topological full groups of minimal subshifts and quantifying local embeddings into finite groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1492-1510
- Print publication:
- May 2023
-
- Article
- Export citation
The BNSR-invariants of the Lodha–Moore groups, and an exotic simple group of type
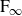 $\textrm{F}_\infty$
$\textrm{F}_\infty$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 April 2022, pp. 25-48
- Print publication:
- January 2023
-
- Article
- Export citation