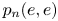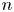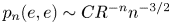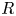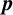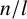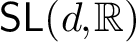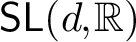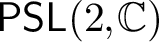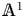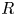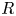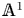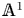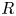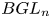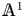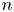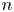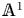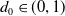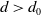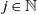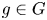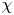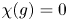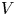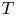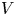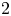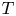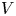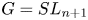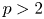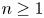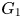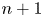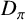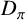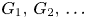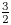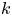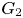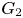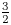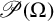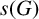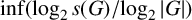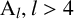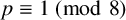Refine listing
Actions for selected content:
1959 results in 20xxx
Local limit theorems in relatively hyperbolic groups II: the non-spectrally degenerate case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 764-830
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Grothendieck–Serre in the quasi-split unramified case
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 March 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONJUGACY CLASSES OF MAXIMAL CYCLIC SUBGROUPS AND NILPOTENCE CLASS OF
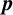 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 463-469
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERSECTION OF CONJUGATE SOLVABLE SUBGROUPS IN FINITE CLASSICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 507-510
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
QUASI-ISOMETRIC EMBEDDINGS INAPPROXIMABLE BY ANOSOV REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 2497-2514
- Print publication:
- September 2023
-
- Article
- Export citation
Localization and nilpotent spaces in
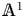 ${\mathbb {A}}^1$-homotopy theory
${\mathbb {A}}^1$-homotopy theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 654-720
- Print publication:
- March 2022
-
- Article
- Export citation
Overgroups of regular unipotent elements in reductive groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 February 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Property (T) in k-gonal random groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 734-738
- Print publication:
- September 2022
-
- Article
- Export citation
On finite groups with exactly one vanishing conjugacy class size
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 344-368
- Print publication:
- February 2023
-
- Article
- Export citation
Packable hyperbolic surfaces with symmetries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 103-113
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irrational-slope versions of thompson's groups T and V
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 244-262
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuity of critical exponent of quasiconvex-cocompact groups under Gromov–Hausdorff convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 10 February 2022, pp. 1189-1221
- Print publication:
- April 2023
-
- Article
- Export citation
Explicit calculations in an infinitesimal singular block of SLn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 February 2022, pp. 19-52
-
- Article
- Export citation
A NOTE ON WIELANDT’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 310-314
- Print publication:
- October 2022
-
- Article
- Export citation
On the spread of infinite groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 214-228
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOHR COMPACTIFICATIONS OF GROUPS AND RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1103-1137
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thermodynamic metrics on outer space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 729-793
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF SET ORBITS OF PERMUTATION GROUPS AND THE GROUP ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 27 January 2022, pp. 89-101
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE TWO-DISTANCE-TRANSITIVE DIHEDRANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 386-401
- Print publication:
- December 2022
-
- Article
- Export citation
A NOTE ON ÉTALE REPRESENTATIONS FROM NILPOTENT ORBITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 25 January 2022, pp. 113-125
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation