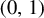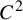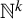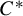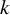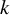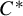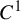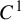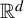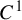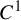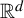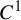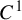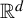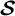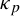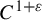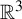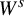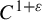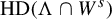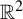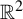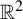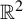Contents
Original Article
Quasisymmetric orbit-flexibility of multicritical circle maps
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3271-3310
-
- Article
- Export citation
Examples of distorted interval diffeomorphisms of intermediate regularity
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3311-3324
-
- Article
- Export citation
Cocycles on groupoids arising from
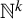 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dimension estimates for
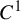 $C^1$ iterated function systems and repellers. Part II
$C^1$ iterated function systems and repellers. Part II
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3357-3392
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
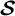 $\mathcal{\textbf{S}}$-adic characterization of minimal ternary dendric shifts
$\mathcal{\textbf{S}}$-adic characterization of minimal ternary dendric shifts
- Part of:
-
- Published online by Cambridge University Press:
- 02 September 2021, pp. 3393-3432
-
- Article
- Export citation
Chaotic behavior of the p-adic Potts–Bethe mapping II
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3433-3457
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff and packing dimensions and measures for nonlinear transversally non-conformal thin solenoids
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3458-3489
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicative constants and maximal measurable cocycles in bounded cohomology
- Part of:
-
- Published online by Cambridge University Press:
- 31 August 2021, pp. 3490-3525
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topologically mixing tiling of
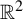 $\mathbb {R}^2$ generated by a generalized substitution
$\mathbb {R}^2$ generated by a generalized substitution
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3526-3550
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 42 issue 11 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 October 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 42 issue 11 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 October 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation