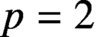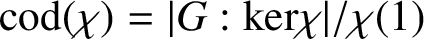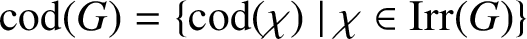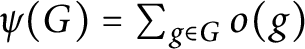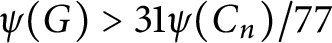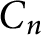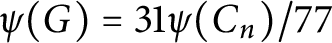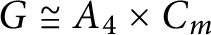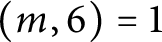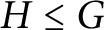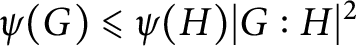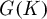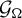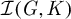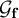Refine listing
Actions for selected content:
1959 results in 20xxx
ON GRAEV’S THEOREM FOR FREE PRODUCTS OF HAUSDORFF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 475-483
- Print publication:
- December 2021
-
- Article
- Export citation
CONNECTED COMPONENTS IN THE INVARIABLY GENERATING GRAPH OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 25 March 2021, pp. 453-463
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
2-dimensional Coxeter groups are biautomatic
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 382-401
- Print publication:
- April 2022
-
- Article
- Export citation
GROUPS OF WORLDVIEW TRANSFORMATIONS IMPLIED BY EINSTEIN’S SPECIAL PRINCIPLE OF RELATIVITY OVER ARBITRARY ORDERED FIELDS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 334-361
- Print publication:
- June 2022
-
- Article
- Export citation
Local limit theorems in relatively hyperbolic groups I: rough estimates
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 1926-1966
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 1947-1999
- Print publication:
- November 2022
-
- Article
- Export citation
Rigid automorphisms of linking systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 March 2021, e23
-
- Article
-
- You have access
- Open access
- Export citation
Higher horospherical limit sets for G-modules over CAT(0)-spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 12 March 2021, pp. 133-163
- Print publication:
- July 2021
-
- Article
- Export citation
THE CENTER OF SL2 TILTING MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 165-184
- Print publication:
- January 2022
-
- Article
- Export citation
LOCAL COORDINATES FOR COMPLEX AND QUATERNIONIC HYPERBOLIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 57-78
- Print publication:
- August 2022
-
- Article
- Export citation
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 March 2021, pp. 545-566
- Print publication:
- June 2022
-
- Article
- Export citation
STRONGLY BOUNDED LOCALLY INDICABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 443-447
- Print publication:
- December 2021
-
- Article
- Export citation
Divergence and quasi-isometry classes of random Gromov’s monsters
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 18 February 2021, pp. 249-264
- Print publication:
- September 2021
-
- Article
- Export citation
The fields of values of characters of degree not divisible by p
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 February 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
AN ANALOGUE OF HUPPERT’S CONJECTURE FOR CHARACTER CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 278-286
- Print publication:
- October 2021
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
Low-dimensional representations of finite orthogonal groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 26 January 2021, pp. 585-606
- Print publication:
- November 2021
-
- Article
- Export citation
On two conjectures about the sum of element orders
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 January 2021, pp. 30-38
- Print publication:
- March 2022
-
- Article
- Export citation
IHARA LEMMA AND LEVEL RAISING IN HIGHER DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1701-1726
- Print publication:
- September 2022
-
- Article
- Export citation
THÉORIE DE BRUHAT-TITS POUR LES GROUPES QUASI-RÉDUCTIFS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1331-1362
- Print publication:
- July 2022
-
- Article
- Export citation