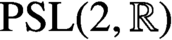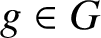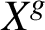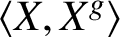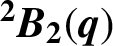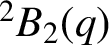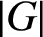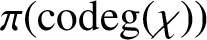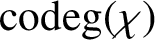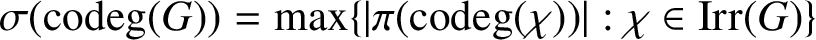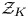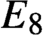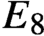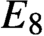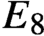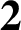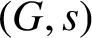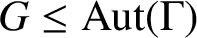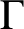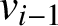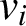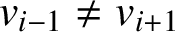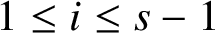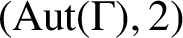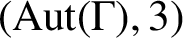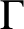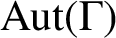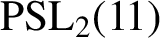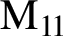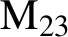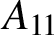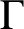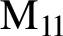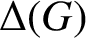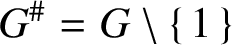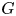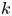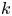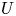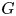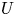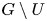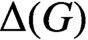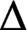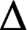Refine listing
Actions for selected content:
1959 results in 20xxx
ON GOOD APPROXIMATIONS AND THE BOWEN–SERIES EXPANSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 25 January 2021, pp. 45-58
- Print publication:
- August 2021
-
- Article
- Export citation
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 1677-1700
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE PRONORM OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 287-294
- Print publication:
- October 2021
-
- Article
- Export citation
EXTREMAL CASES OF RAPOPORT–ZINK SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 20 January 2021, pp. 1727-1782
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- Export citation
COPRIME COMMUTATORS IN THE SUZUKI GROUPS
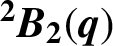 $^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
$^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 448-452
- Print publication:
- December 2021
-
- Article
- Export citation
ON ANALOGUES OF HUPPERT’S CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 272-277
- Print publication:
- October 2021
-
- Article
- Export citation
One-relator groups and algebras related to polyhedral products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 15 January 2021, pp. 128-147
- Print publication:
- February 2022
-
- Article
- Export citation
A class of continuous non-associative algebras arising from algebraic groups including
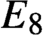 $E_8$
$E_8$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 14 January 2021, e6
-
- Article
-
- You have access
- Open access
- Export citation
LECTURES ON THE GEOMETRY AND MODULAR REPRESENTATION THEORY OF ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 January 2021, pp. 1-47
- Print publication:
- February 2021
-
- Article
- Export citation
FACTORIZATION LENGTH DISTRIBUTION FOR AFFINE SEMIGROUPS III: MODULAR EQUIDISTRIBUTION FOR NUMERICAL SEMIGROUPS WITH ARBITRARILY MANY GENERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 12 January 2021, pp. 21-35
- Print publication:
- August 2022
-
- Article
- Export citation
NEW CONSTRUCTIONS OF SELF-COMPLEMENTARY CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 372-385
- Print publication:
- December 2021
-
- Article
- Export citation
CLASSIFICATION OF TETRAVALENT
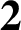 $\textbf{2}$-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS
$\textbf{2}$-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 263-271
- Print publication:
- October 2021
-
- Article
- Export citation
On exceptional Lie geometries
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
Minimal rational curves on generalized Bott–Samelson varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 122-153
- Print publication:
- January 2021
-
- Article
- Export citation
THE CYCLIC GRAPH OF A Z-GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 295-301
- Print publication:
- October 2021
-
- Article
- Export citation
FINITE p-GROUPS AND COCLASS THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 164-166
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
ACYLINDRICAL HYPERBOLICITY OF ARTIN–TITS GROUPS ASSOCIATED WITH TRIANGLE-FREE GRAPHS AND CONES OVER SQUARE-FREE BIPARTITE GRAPHS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 01 December 2020, pp. 51-64
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Arithmetic purity of strong approximation for semi-simple simply connected groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 01 February 2021, pp. 2628-2649
- Print publication:
- December 2020
-
- Article
- Export citation
A cancellation theorem for modules over integral group rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 27 November 2020, pp. 317-327
- Print publication:
- September 2021
-
- Article
- Export citation
THE CHARACTER GRAPH OF A FINITE GROUP IS PERFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 127-131
- Print publication:
- August 2021
-
- Article
- Export citation