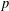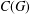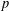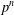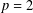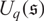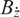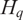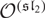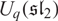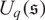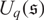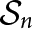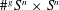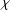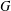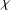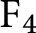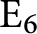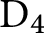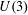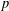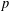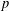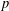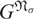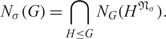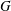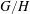Refine listing
Actions for selected content:
1959 results in 20xxx
THE SECOND MINIMUM/MAXIMUM VALUE OF THE NUMBER OF CYCLIC SUBGROUPS OF FINITE
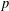 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 April 2020, pp. 96-103
- Print publication:
- February 2021
-
- Article
- Export citation
BGG CATEGORY FOR THE QUANTUM SCHRÖDINGER ALGEBRA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 20 April 2020, pp. 266-279
- Print publication:
- May 2021
-
- Article
- Export citation
CLASSIFICATION OF THE SUBLATTICES OF A LATTICE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 50-61
- Print publication:
- February 2021
-
- Article
- Export citation
Gelfand Pairs Involving the Wreath Product of Finite Abelian Groups with Symmetric Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 91-97
- Print publication:
- March 2021
-
- Article
- Export citation
ON THE COHOMOLOGY OF TORELLI GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 April 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
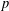 $p$-DIVISIBILITY OF CO-DEGREES OF IRREDUCIBLE CHARACTERS
$p$-DIVISIBILITY OF CO-DEGREES OF IRREDUCIBLE CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 07 April 2020, pp. 78-82
- Print publication:
- February 2021
-
- Article
- Export citation
Factorization problems in complex reflection groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 899-946
- Print publication:
- August 2021
-
- Article
- Export citation
Orders on Trees and Free Products of Left-ordered Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 31 March 2020, pp. 335-347
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Albert algebras over rings and related torsors
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 875-898
- Print publication:
- June 2021
-
- Article
- Export citation
SERRE WEIGHTS AND BREUIL’S LATTICE CONJECTURE IN DIMENSION THREE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 25 March 2020, e5
-
- Article
-
- You have access
- Open access
- Export citation
Relative cubulations and groups with a 2-sphere boundary
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 862-867
- Print publication:
- April 2020
-
- Article
- Export citation
Stability in the high-dimensional cohomology of congruence subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 822-861
- Print publication:
- April 2020
-
- Article
- Export citation
GROUPS WITH NORMALITY CONDITIONS FOR UNCOUNTABLE SUBGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 268-277
- Print publication:
- October 2021
-
- Article
- Export citation
FINITE GROUPS WITH COMPLEMENTED 2-MINIMAL
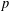 $p$-SUBGROUPS
$p$-SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 11 March 2020, pp. 430-438
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Affine Hecke algebras and generalizations of quiver Hecke algebras of type B
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 09 March 2020, pp. 531-578
-
- Article
- Export citation
A combination theorem for combinatorially non-positively curved complexes of hyperbolic groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 445-477
- Print publication:
- May 2021
-
- Article
- Export citation
Generation of relative commutator subgroups in Chevalley groups. II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 02 March 2020, pp. 497-511
-
- Article
- Export citation
GRAPH IMMERSIONS, INVERSE MONOIDS AND DECK TRANSFORMATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 02 March 2020, pp. 37-55
- Print publication:
- August 2021
-
- Article
- Export citation
ON THE σ-NILPOTENT NORM AND THE σ-NILPOTENT LENGTH OF A FINITE GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 27 February 2020, pp. 121-132
- Print publication:
- January 2021
-
- Article
- Export citation
An Application of Spherical Geometry to Hyperkähler Slices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 February 2020, pp. 687-716
- Print publication:
- June 2021
-
- Article
- Export citation