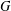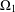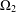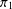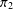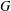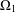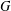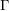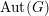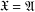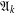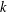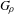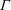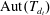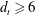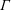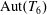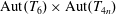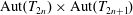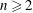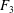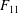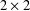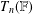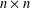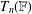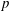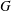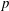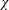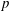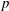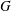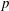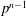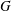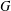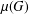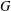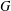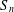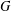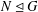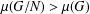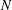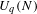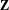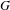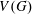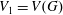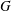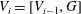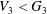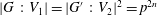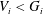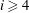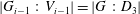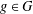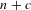Refine listing
Actions for selected content:
1959 results in 20xxx
ON A CONJECTURE ON THE PERMUTATION CHARACTERS OF FINITE PRIMITIVE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 22 October 2019, pp. 77-90
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Bounding the covolume of lattices in products
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 11 October 2019, pp. 2296-2333
- Print publication:
- December 2019
-
- Article
- Export citation
GROUPS WHOSE NONNORMAL SUBGROUPS ARE METAHAMILTONIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 96-103
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Uniformly perfect finitely generated simple left orderable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 08 October 2019, pp. 534-552
- Print publication:
- February 2021
-
- Article
- Export citation
New Simple Lattices in Products of Trees and their Projections
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 October 2019, pp. 1624-1690
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
THE FINITE BASIS PROBLEM FOR INVOLUTION SEMIGROUPS OF TRIANGULAR
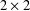 $2\times 2$ MATRICES
$2\times 2$ MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 88-104
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
QUANTUM INCREASING SEQUENCES GENERATE QUANTUM PERMUTATION GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 631-639
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Character Codegrees of Maximal Class
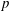 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 25 September 2019, pp. 328-334
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
TAME BLOCK ALGEBRAS OF HECKE ALGEBRAS OF CLASSICAL TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 September 2019, pp. 179-201
- Print publication:
- October 2021
-
- Article
- Export citation
SUBGROUPS WITH NO ABELIAN COMPOSITION FACTORS ARE NOT DISTINGUISHED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 446-452
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
FREE FINITE GROUP ACTIONS ON RATIONAL HOMOLOGY 3-SPHERES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 September 2019, e28
-
- Article
-
- You have access
- Open access
- Export citation
Type classification of extreme quantized characters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 593-605
- Print publication:
- February 2021
-
- Article
- Export citation
FINITE SOLVABLE GROUPS WITH DISTINCT MONOMIAL CHARACTER DEGREES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 04 September 2019, pp. 387-401
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Residually finite tubular groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 August 2019, pp. 2937-2951
- Print publication:
- December 2020
-
- Article
- Export citation
A Tits alternative for topological full groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 622-640
- Print publication:
- February 2021
-
- Article
- Export citation
New Facts about the Vanishing Off Subgroup
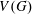 $V(G)$
$V(G)$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 262-268
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
VIRTUALLY FIBERING RIGHT-ANGLED COXETER GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 23 August 2019, pp. 957-987
- Print publication:
- May 2021
-
- Article
- Export citation
ON DISCRETENESS OF SUBGROUPS OF QUATERNIONIC HYPERBOLIC ISOMETRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 16 August 2019, pp. 283-293
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Quasi-Sturmian colorings on regular trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3403-3419
- Print publication:
- December 2020
-
- Article
- Export citation
CONJUGATING AUTOMORPHISMS OF GRAPH PRODUCTS: KAZHDAN’S PROPERTY (T) AND SQ-UNIVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 272-282
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation