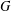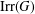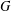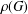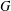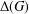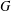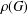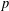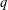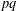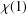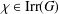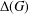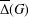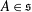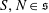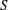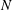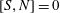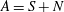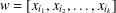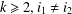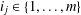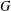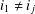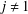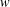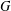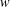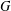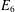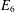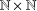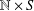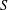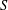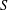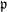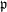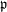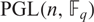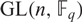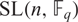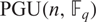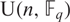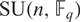Refine listing
Actions for selected content:
1959 results in 20xxx
Profinite groups with restricted centralizers of commutators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 01 April 2019, pp. 2301-2321
- Print publication:
- October 2020
-
- Article
- Export citation
MONOLITHIC BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 434-439
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
2-chains and square roots of Thompson’s group
 $F$
$F$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2515-2532
- Print publication:
- September 2020
-
- Article
- Export citation
Hyperfiniteness of boundary actions of cubulated hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2453-2466
- Print publication:
- September 2020
-
- Article
- Export citation
Cohen–Lenstra heuristics for étale group schemes and symplectic pairings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 758-775
- Print publication:
- April 2019
-
- Article
- Export citation
EXPLICIT cocycle formulas on finite abelian groups with applications to braided linear Gr-categories and Dijkgraaf–Witten invariants
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 1937-1964
- Print publication:
- August 2020
-
- Article
- Export citation
Topos points of quasi-coherent sheaves over monoid schemes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 31-74
- Print publication:
- July 2020
-
- Article
- Export citation
ON THE REGULARITY OF CHARACTER DEGREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 428-433
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Jordan–Chevalley Decomposition in Lie Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 28 February 2019, pp. 349-354
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A NILPOTENCY CRITERION FOR SOME VERBAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 281-289
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ALGEBRAS OF GENERALIZED DIHEDRAL TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 181-236
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
The Conjugacy Ratio of Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 22 February 2019, pp. 895-911
-
- Article
-
- You have access
- Export citation
A generalisation of von Staudt’s theorem on cross-ratios
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 22 February 2019, pp. 601-612
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
CENTRALIZERS OF p-SUBGROUPS IN SIMPLE LOCALLY FINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 February 2019, pp. 183-186
- Print publication:
- January 2020
-
- Article
-
- You have access
- Open access
- Export citation
Multi-GGS Groups have the Congruence Subgroup Property
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 21 February 2019, pp. 889-894
-
- Article
- Export citation
COMPATIBLE SYSTEMS OF GALOIS REPRESENTATIONS ASSOCIATED TO THE EXCEPTIONAL GROUP
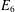 $E_{6}$
$E_{6}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 06 February 2019, e4
-
- Article
-
- You have access
- Open access
- Export citation
ON THE NUMBER OF SUBSEMIGROUPS OF DIRECT PRODUCTS INVOLVING THE FREE MONOGENIC SEMIGROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 24-35
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Local duality for representations of finite group schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 424-453
- Print publication:
- February 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 93-107
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
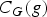
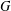
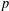
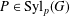
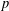
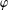
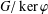
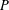
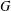
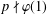


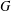
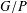



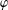
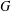

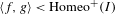
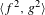

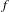

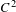
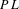

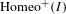
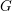
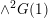
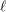
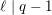
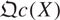 of quasi-coherent sheaves over
of quasi-coherent sheaves over 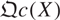 is of this form if
is of this form if 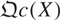 and
and 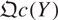 are equivalent.
are equivalent.