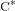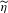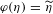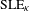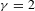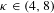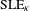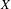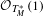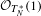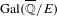Contents
Research Article
CARTAN SUBALGEBRAS IN DIMENSION DROP ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2019, pp. 725-755
-
- Article
-
- You have access
- Open access
- Export citation
UNIQUENESS OF THE WELDING PROBLEM FOR SLE AND LIOUVILLE QUANTUM GRAVITY
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2019, pp. 757-783
-
- Article
- Export citation
ZERO-POINTED MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 02 July 2019, pp. 785-858
-
- Article
- Export citation
ON LOCAL ENERGY DECAY ESTIMATE OF THE OSEEN SEMIGROUP IN TWO DIMENSIONS AND ITS APPLICATION
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2019, pp. 859-891
-
- Article
- Export citation
INVARIANCE OF THE GERSTENHABER ALGEBRA STRUCTURE ON TATE-HOCHSCHILD COHOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2019, pp. 893-928
-
- Article
- Export citation
EQUIVARIANT ALGEBRAIC INDEX THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 929-955
-
- Article
- Export citation
VIRTUALLY FIBERING RIGHT-ANGLED COXETER GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 23 August 2019, pp. 957-987
-
- Article
- Export citation
LINEAR INDEPENDENCE IN THE RATIONAL HOMOLOGY COBORDISM GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 28 August 2019, pp. 989-1000
-
- Article
- Export citation
TATE’S CONJECTURE AND THE TATE–SHAFAREVICH GROUP OVER GLOBAL FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2019, pp. 1001-1022
-
- Article
- Export citation
RC-POSITIVITY, VANISHING THEOREMS AND RIGIDITY OF HOLOMORPHIC MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1023-1038
-
- Article
- Export citation
HEREDITARILY ANTISYMMETRIC OPERATOR ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2019, pp. 1039-1074
-
- Article
- Export citation
GALOIS CONJUGATES OF SPECIAL POINTS AND SPECIAL SUBVARIETIES IN SHIMURA VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 30 October 2019, pp. 1075-1089
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 20 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 May 2021, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 20 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 May 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation