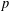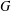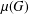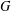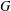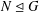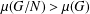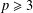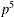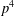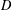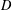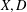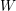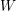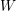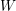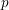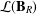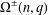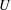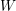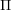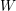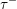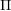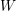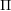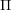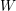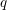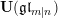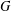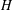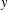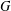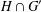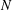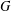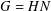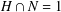Refine listing
Actions for selected content:
1959 results in 20xxx
ON VANISHING CRITERIA THAT CONTROL FINITE GROUP STRUCTURE II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 251-257
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
MINIMAL EXCEPTIONAL
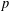 $p$ -GROUPS
$p$ -GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 434-438
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
CONTINUOUS ASSOCIATION SCHEMES AND HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 July 2018, pp. 361-426
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ON CANONICAL BASES AND INDUCTION OF
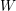 $W$-GRAPHS
$W$-GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 17 July 2018, pp. 1-41
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
INTERTWINING SEMISIMPLE CHARACTERS FOR
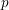 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 16 July 2018, pp. 137-205
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
A STRUCTURED DESCRIPTION OF THE GENUS SPECTRUM OF ABELIAN p-GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 10 July 2018, pp. 381-423
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
EXHAUSTION OF THE CURVE GRAPH VIA RIGID EXPANSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 July 2018, pp. 195-230
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
MODULAR DECOMPOSITION NUMBERS OF CYCLOTOMIC HECKE AND DIAGRAMMATIC CHEREDNIK ALGEBRAS: A PATH THEORETIC APPROACH
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 03 July 2018, e11
-
- Article
-
- You have access
- Open access
- Export citation
ON PAIRED ROOT SYSTEMS OF COXETER GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 347-365
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
ON PSEUDO-EHRESMANN SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 257-288
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
THE LATTICE OF VARIETIES OF STRICT LEFT RESTRICTION SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 May 2018, pp. 31-55
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON SEMIGROUPS WITH PSPACE-COMPLETE SUBPOWER MEMBERSHIP PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 May 2018, pp. 127-142
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON INVOLUTIONS AND INDICATORS OF FINITE ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 380-416
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
LOCAL SYSTEMS ON COMPLEMENTS OF ARRANGEMENTS OF SMOOTH, COMPLEX ALGEBRAIC HYPERSURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 May 2018, e6
-
- Article
-
- You have access
- Open access
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
- Export citation
INTERSECTIONS OF MULTICURVES FROM DYNNIKOV COORDINATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 149-158
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
MULTIPLICATION FORMULAS AND SEMISIMPLICITY FOR
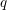 $q$-SCHUR SUPERALGEBRAS
$q$-SCHUR SUPERALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 98-126
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
Homological vanishing for the Steinberg representation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 1111-1130
- Print publication:
- June 2018
-
- Article
- Export citation
A NOTE ON NORMAL COMPLEMENTS FOR FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 109-112
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Maximal Subgroups and Irreducible Representations of Generalized Multi-Edge Spinal Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 673-703
-
- Article
- Export citation