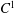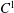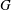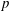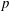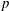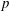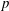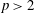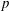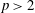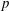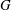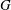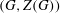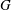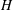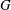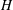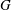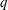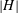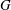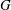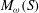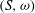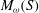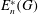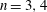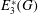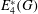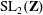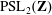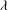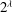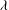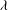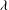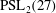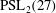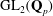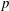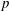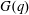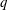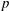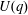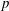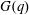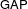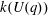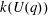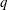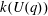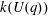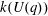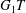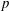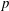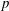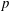Refine listing
Actions for selected content:
1959 results in 20xxx
THE JOIN OF SPLIT GRAPHS WHOSE QUASI-STRONG ENDOMORPHISMS FORM A MONOID
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 June 2014, pp. 1-10
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Sur les rapprochements par conjugaison en dimension 1 et classe
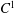 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 19 June 2014, pp. 1183-1195
- Print publication:
- July 2014
-
- Article
- Export citation
FINITELY ANNIHILATED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 404-417
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A GROUP SUM INEQUALITY AND ITS APPLICATION TO POWER GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 418-426
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The
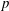 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
NONINNER AUTOMORPHISMS OF ORDER
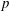 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ IN FINITE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ IN FINITE 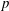 $p$-GROUPS OF COCLASS 2, WHEN
$p$-GROUPS OF COCLASS 2, WHEN 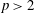 $p>2$
$p>2$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 232-236
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON THE FORMAL AFFINE HECKE ALGEBRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 09 June 2014, pp. 837-855
- Print publication:
- October 2015
-
- Article
- Export citation
ON NONINNER 2-AUTOMORPHISMS OF FINITE 2-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 29 May 2014, pp. 227-231
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON A CLASS OF SUPERSOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 23 May 2014, pp. 220-226
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
GLOBAL DETERMINISM OF CLIFFORD SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 16 May 2014, pp. 63-77
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
THE MULTIPLIER ALGEBRA OF A BEURLING ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 113-120
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF P. HALL FOR ENGEL WORDS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 237-246
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
ON SOLUBILITY OF GROUPS WITH FEW NORMALISERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 247-249
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Congruence testing for odd subgroups of the modular group
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 206-208
-
- Article
-
- You have access
- Export citation
SMALL DOUBLING IN ORDERED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 30 April 2014, pp. 316-325
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
FREE GROUPS AND AUTOMORPHISM GROUPS OF INFINITE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 17 April 2014, e8
-
- Article
-
- You have access
- Open access
- Export citation
Classification of subgroups isomorphic to
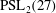 $\mathrm{PSL}_2(27)$ in the Monster
$\mathrm{PSL}_2(27)$ in the Monster
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 33-46
-
- Article
-
- You have access
- Export citation
Computing fundamental domains for the Bruhat–Tits tree for
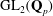 ${\rm GL}_2(\mathbf{Q}_p)$ ,
${\rm GL}_2(\mathbf{Q}_p)$ , 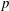 $p$ -adic automorphic forms, and the canonical embedding of Shimura curves
$p$ -adic automorphic forms, and the canonical embedding of Shimura curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 1-23
-
- Article
-
- You have access
- Export citation
Calculating conjugacy classes in Sylow
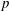 $p$ -subgroups of finite Chevalley groups of rank six and seven
$p$ -subgroups of finite Chevalley groups of rank six and seven
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 109-122
-
- Article
-
- You have access
- Export citation
Loewy series of parabolically induced
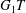 $G_1T$ -Verma modules
$G_1T$ -Verma modules
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 March 2014, pp. 185-220
- Print publication:
- January 2015
-
- Article
- Export citation