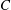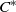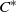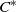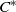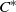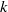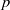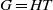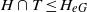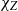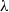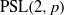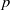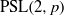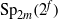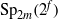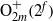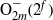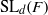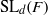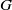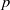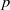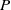Refine listing
Actions for selected content:
1959 results in 20xxx
Abstract simplicity of locally compact Kac–Moody groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 713-728
- Print publication:
- April 2014
-
- Article
- Export citation
Finiteness properties of cubulated groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 453-506
- Print publication:
- March 2014
-
- Article
- Export citation
JOINS AND COVERS IN INVERSE SEMIGROUPS AND TIGHT
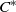 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 121-133
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Infinite presentability of groups and condensation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 811-848
- Print publication:
- October 2014
-
- Article
- Export citation
(STRONGLY) GORENSTEIN FLAT MODULES OVER GROUP RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 17 December 2013, pp. 57-64
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Modular Koszul duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 13 December 2013, pp. 273-332
- Print publication:
- February 2014
-
- Article
- Export citation
Pro-
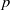 $\lowercase p$ Iwahori–Hecke algebras are Gorenstein
$\lowercase p$ Iwahori–Hecke algebras are Gorenstein
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 28 November 2013, pp. 753-809
- Print publication:
- October 2014
-
- Article
- Export citation
FINITE
 $s$-GEODESIC TRANSITIVE GRAPHS
$s$-GEODESIC TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 November 2013, pp. 175-176
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
LOCALLY FINITE GROUPS WHOSE SUBGROUPS HAVE FINITE NORMAL OSCILLATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 20 November 2013, pp. 479-487
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
STRONGLY ORTHODOX CONGRUENCES ON AN
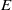 $E$-INVERSIVE SEMIGROUP
$E$-INVERSIVE SEMIGROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 216-230
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
SOME NEW CHARACTERISATIONS OF FINITE
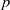 $p$-SUPERSOLUBLE GROUPS
$p$-SUPERSOLUBLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 08 November 2013, pp. 514-521
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Computing characters of groups with central subgroups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 07 November 2013, pp. 398-406
-
- Article
-
- You have access
- Export citation
The minimal generating sets of
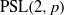 $\mathrm{PSL} (2, p)$ of size four
$\mathrm{PSL} (2, p)$ of size four
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 06 November 2013, pp. 419-423
-
- Article
-
- You have access
- Export citation
Braid group actions via categorifiedHeisenberg complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 09 October 2013, pp. 105-142
- Print publication:
- January 2014
-
- Article
- Export citation
A REMARK ON THE PERMUTATION REPRESENTATIONS AFFORDED BY THE EMBEDDINGS OF
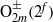 ${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN
${ \text{O} }_{2m}^{\pm } ({2}^{f} )$ IN 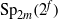 ${\text{Sp} }_{2m} ({2}^{f} )$
${\text{Sp} }_{2m} ({2}^{f} )$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 19 September 2013, pp. 331-336
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
CANNON–THURSTON MAPS DO NOT ALWAYS EXIST
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 11 September 2013, e3
-
- Article
-
- You have access
- Open access
- Export citation
THE ZELEZNIKOW PROBLEM ON A CLASS OF ADDITIVELY IDEMPOTENT SEMIRINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 05 September 2013, pp. 404-420
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
MIXING FOR PROGRESSIONS IN NONABELIAN GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 29 August 2013, e2
-
- Article
-
- You have access
- Open access
- Export citation
A NOTE ON THE WEISS CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 356-361
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
SPECIAL MAXIMAL SUBGROUPS OF
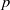 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 415-419
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation