Refine listing
Actions for selected content:
1959 results in 20xxx
The group of endotrivial modules for the symmetric and alternating groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 83-95
-
- Article
-
- You have access
- Export citation
Properties of soluble groups detectable at their metabelian subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 31-38
-
- Article
-
- You have access
- Export citation
Simplicial cohomology of augmentation ideals in l1(G)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 97-109
-
- Article
-
- You have access
- Export citation
Zero-cycles on projective varieties and the norm principle
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 23 December 2009, pp. 457-464
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
GROUPS WITH ABELIAN SYLOW SUBGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 16 December 2009, pp. 43-47
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF PRIME ORDER SUBGROUPS OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 329-357
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Multiplicative Invariants and the Finite Co-Hopfian Property
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 115-127
- Print publication:
- December 2009
-
- Article
- Export citation
REES MATRIX CONSTRUCTIONS FOR CLUSTERING OF DATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 377-393
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
GROUP ALGEBRAS WHOSE GROUP OF UNITS IS POWERFUL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 325-328
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Whittaker unitary dual of affine graded Hecke algebras of type E
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1563-1616
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
GRAPH PRODUCTS OF RIGHT CANCELLATIVE MONOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 227-252
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Leading coefficients and cellular bases of Hecke algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 653-677
-
- Article
-
- You have access
- Export citation
Combinatorial Gelfand models for some semigroups and q-rook monoid algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 707-718
-
- Article
-
- You have access
- Export citation
COMBINATORIAL REES–SUSHKEVICH VARIETIES THAT ARE CROSS, FINITELY GENERATED, OR SMALL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 13 August 2009, pp. 64-84
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group. III
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 431-448
- Print publication:
- April 2010
-
- Article
- Export citation
GENERAL THEOREMS ON AUTOMORPHISMS OF SEMIGROUPS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1-17
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
OVERGROUPS OF PRIMITIVE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 37-82
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
ENDS FOR MONOIDS AND SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 01 August 2009, pp. 101-127
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
THE TILING SEMIGROUPS OF ONE-DIMENSIONAL PERIODIC TILINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 23 July 2009, pp. 153-160
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
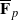 -representation
-representation 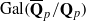 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(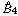 . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.
. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.